Saving lives in normal times is better to improve the longterm future than doing so in catastrophes?

By Vasco Grilo🔸 @ 2024-04-20T08:37 (+11)

You can give me anonymous feedback about anything you want here.

Summary

• Interventions in the effective altruism community are usually assessed under 2 different frameworks, existential risk mitigation, and nearterm welfare improvement. It looks like 2 distinct frameworks are needed given the difficulty of comparing nearterm and longterm effects. However, I do not think this is quite the right comparison under a longtermist perspective, where most of the expected value of one’s actions results from influencing the longterm future, and the indirect longterm effects of saving lives outside catastrophes cannot be neglected.
• In this case, I believe it is better to use a single framework for assessing interventions saving human lives in catastrophes and normal times. One way of doing this, which I consider in this post, is supposing the benefits of saving one life are a function of the population size.
• Assuming the benefits of saving a life are proportional to the ratio between the initial and final population, and that the cost to save a life does not depend on this ratio, it looks like saving lives in normal times is better to improve the longterm future than doing so in catastrophes.
• Many in the effective altruism community argue for focussing on existential risk mitigation given its high neglectedness relative to its importance, i.e. high ratio between potential (astronomical) benefits and (tiny) amount of resources currently being dedicated to it. However, this does not appear to be the right measure of whether a problem is neglected in the relevant sense. One has to consider not only the benefits of solving a problem, but also multiply these by their probability, and arguably expect spending to be proportional to the product.
• The above is in contrast to Nick Bostrom’s maxipok rule.
  • I question this as follows under my framework:
    • The benefits of saving a life tend to infinity as the post-catastrophe population goes to 0, i.e. as one is increasingly confident it would cause human extinction.
    • Yet, the probability of the severity of a catastrophe tends to 0 as severity increases.
    • The 2 points above have opposing effects in terms of the expected value of saving a human life, and one cannot consider each of them in isolation because they are not independent.
    • I think the expected value of saving a human life tends to 0 under reasonable assumptions as the severity of the catastrophe increases.
  • As a 1st approximation, I believe all interventions could be fairly assessed based on a single metric like the number of disability-adjusted life years averted per dollar, as calculated through a standard cost-effectiveness analysis.

Introduction

Interventions in the effective altruism community are usually assessed under 2 different frameworks:

• Existential risk mitigation, where the goal is often decreasing extinction or global catastrophic risk associated with catastrophes in the next few decades. For example, the interventions supported by the Long-Term Future Fund (LTFF).
• Nearterm welfare improvement, where the goal is improving the lives of animals or humans in the next few decades. For example, the interventions supported by the Animal Welfare Fund and GiveWell’s funds.

In agreement with the above and its commitment to worldview diversification, Open Philanthropy says:

So far, the focus areas we have selected fall into one of two broad categories: Global Health and Wellbeing (GHW) and Global Catastrophic Risks (GCR). We summarize the key differences between these portfolios as follows:

• While GCR grants tend to be evaluated based on something like “How much this grant reduces the chance of a catastrophic event that endangers billions of people”, GHW grants tend to be evaluated based on something like “How much this grant increases health (denominated in e.g. life-years) and/or wellbeing, worldwide.”
• The GHW team places greater weight on evidence, precedent, and track record in its giving; the GCR team tends to focus on problems and interventions where evidence and track records are often comparatively thin. (That said, the GHW team does support a significant amount of low-probability but high-upside work like policy advocacy and scientific research.)
• The GCR team’s work could be hugely important, but it’s very hard to answer questions like “How will we know whether this work is on track to have an impact?” We can track intermediate impacts and learn to some degree, but some key premises likely won’t become very clear for decades or more. (Our primary goal is for catastrophic events not to happen, and to the extent we succeed, it can be hard to learn from the absence of events.) By contrast, we generally expect the work of the GHW team to be more likely to result in recognizable impact on a given ~10-year time frame, and to be more amenable to learning and changing course as we go.

It looks like 2 distinct frameworks are needed given the difficulty of comparing nearterm and longterm effects. However, I do not think this is quite the right comparison under a longtermist perspective, where most of the expected value of one’s actions results from influencing the longterm future, and the indirect longterm effects of saving lives outside catastrophes cannot be neglected. In this case, I believe it is better to use a single framework for assessing interventions saving human lives in catastrophes and normal times. One way of doing this, which I consider in this post, is supposing the benefits of saving one life are a function of the population size.

Note Rethink Priorities’ cross-cause cost-effectiveness model (CCM) also estimates the cost-effectiveness of interventions in the 2 aforementioned categories under the same metric (DALY/$). Nevertheless, I would say it underestimates the benefits of saving lives in normal times by neglecting their indirect longterm effects, which should be considered if one holds a longtermist view.

Expected value density of the benefits and cost-effectiveness of saving a life

Denoting the population at the start and end of any period of 1 year (e.g. a calendar year) by $P_i$ and $P_f$, which I will refer to as the initial and final population, I assume:

• $P_i/P_f$ follows a Pareto distribution (power law), which means its probability density function (PDF) is $f=\alpha {\left(P_i/P_f\right)}^{-(\alpha +1)}$, where $\alpha >0$ is the tail index.
  • Given the probability of $P_i/P_f$ being higher than a given ratio $r$ is $p=r^{-\alpha }$, one can determine $\alpha$ from $p_1/p_2={\left(r_1/r_2\right)}^{-\alpha }\iff \alpha =\ln \left(p_1/p_2\right)/\ln \left(r_2/r_1\right)$, where $p_1$ and $p_2$ are the tail risks respecting the ratios $r_1$ and $r_2$.
  • I would not agree with assuming a Pareto distribution for the reduction in population as a fraction of the initial population ($1-P_f/P_i$).
    • This fraction is limited to 1, whereas a Pareto distribution can take an arbitrarily large value.
    • So assuming a Pareto would mean a reduction in population could exceed the initial population, which does not make sense.
• The benefits of saving a life are $B=k_B{\left(P_i/P_f\right)}^{{ϵ}_B}$, where:
  • $k_B$ are the benefits of saving a life in normal times.
  • ${ϵ}_B$ is the elasticity of the benefits with respect to the ratio between the initial and final population.
  • ${ϵ}_B>0$ for the benefits to increase as the final population decreases.
• The cost of saving a life is $C=k_C{\left(P_i/P_f\right)}^{{ϵ}_C}$, where:
  • $k_C$ is the cost to save a life in normal times.
  • ${ϵ}_C$ is the elasticity of the cost with respect to the ratio between the initial and final population.

Consequently, the expected value density of:

• The benefits of saving a life is $fB=\alpha k_B{\left(P_i/P_f\right)}^{{ϵ}_B-\alpha -1}$.
• The cost-effectiveness of saving a life is $fB/C=\alpha \left(k_B/k_C\right){\left(P_i/P_f\right)}^{{ϵ}_B-{ϵ}_C-\alpha -1}$.

I guess:

• ${ϵ}_B=1$, as Carl Shulman seems to suggest in a post on the flow-through effects of saving a life that the respective indirect longterm effects, in terms of the time by which humanity’s trajectory is advanced, are inversely proportional to the population when the life is saved^[1].
• ${ϵ}_C=0$, since I feel like the effect of having more opportunities to save lives over periods with lower final population is roughly offset by the greater difficulty of preparing to take advantage of those opportunities.

As a result, the expected value densities of the benefits and cost-effectiveness of saving a life are both proportional to $\alpha {\left(P_i/P_f\right)}^{-\alpha }$, which tends to 0 as the final population decreases. So it looks like saving lives in normal times is better to improve the longterm future than doing so in catastrophes.

I got values for $\alpha$ of 0.153 (= ln(0.0905/0.01)/ln(2.02*10^6/1.11)) and 0.0835 (= ln(0.20/0.06)/ln(2.02*10^6/1.11)) based on the predictions of the superforecasters and experts of the Existential Risk Persuasion Tournament (XPT) for the global catastrophic and extinction risk between 2023 and 2100:

• Global catastrophic risk refers to more than 10 % of humans dying, so $r_1$ is 1.11 (= 1/(1 - 0.1)).
• Extinction risk refers to less than 5 k people surviving, and the global population is projected to be 10.1 billion in 2061 ((2023 + 2100)/2 = 2061.5), which is in the middle of the relevant period, so $r_2$ is 2.02 M (= 10.1*10^9/(5*10^3)).
• Superforecasters predicted a global catastrophic and extinction risk of $p_1=0.0905$ and $p_2=0.01$, and experts $p_1=0.20$ and $p_2=0.06$ (see Table 1).

For the tail indices I mentioned, the expected value densities of the benefits and cost-effectiveness of saving a life are 34.8 % (= (10^3)^-0.153) and 56.2 % (= (10^3)^-0.0835) as high for a final population 0.1 % (= 10^-3) as large. Nonetheless, I would say the above tail indices are overestimates, as I suspect extinction risk was overestimated in the XPT. The annual risk of human extinction from nuclear war from 2023 to 2050 estimated by the superforecasters, domain experts, general existential risk experts, and non-domain experts of the XPT is 602 k, 7.23 M, 10.3 M and 4.22 M times mine.

The tail index would be 0.313 (= ln(0.0905/0.001)/ln(2.02*10^6/1.11)) for my guess of an extinction risk from 2023 to 2100 of around 0.1 % (essentially from transformative artificial intelligence), and superforecasters’ global catastrophic risk of 9.05 %. In this case, the expected value densities of the benefits and cost-effectiveness of saving a life would be 11.5 % (= (10^3)^-0.313) as high for a final population 0.1 % as large.

Existential risk mitigation is not neglected?

Many in the effective altruism community argue for focussing on existential risk mitigation given its high neglectedness relative to its importance, i.e. high ratio between potential (astronomical) benefits and (tiny) amount of resources currently being dedicated to it. However, this does not appear to be the right measure of whether a problem is neglected in the relevant sense. One has to consider not only the benefits of solving a problem, but also multiply these by their PDF, and arguably expect spending to be proportional to the product, i.e. to the expected value density of the benefits. Focussing on this has implications for what is fairly/unfairly neglected. To illustrate:

• In the context of war deaths, the tail index is “1.35 to 1.74, with a mean of 1.60”. So the PDF of the benefits is proportional to “deaths”^-2.6 (= “deaths”^-(“tail index” + 1)).
• So I think spending should a priori be proportional to “deaths”^-1.6 (= “deaths”*“deaths”^-2.6).
• As a consequence, if the goal is minimising war deaths^[2], spending to save lives in wars 1 k times as deadly should be 0.00158 % (= (10^3)^(-1.6)) as large.

Here is an example of a discussion which apparently does not account for the probability of the benefits being realised. In Founders Pledge’s report Philanthropy to the Right of Boom, Christian Ruhl says:

suppose for the sake of argument that a nuclear terrorist attack could kill 100,000 people, and an all-out nuclear war could kill 1 billion people. All else equal, in this scenario it would be 10,000 times more effective to focus on preventing all-out war than it is to focus on nuclear terrorism.[8]

Here is footnote 8:

All else, obviously, is not equal. Questions about the tractability of escalation management are crucial.

Here is the paragraph following what I quoted above:

Generalizing this pattern, philanthropists ought to prioritize the largest nuclear wars (again, all else equal) when thinking about additional resources at the margin.

However, as I showed, the Pareto distribution describing war deaths is such that the expected value density of deaths decreases with war severity. So, all else equal except for the probability of a war having a given size, it may well be better to address smaller wars.

Here is another example where the probability of the benefits being realised is seemingly not adequately considered. Cotton-Barratt 2020 says “it’s usually best to invest significantly into strengthening all three defence layers”:

• Prevention. “First, how does it start causing damage?”.
• Response. “Second, how does it reach the scale of a global catastrophe?”.
• Resilience. “Third, how does it reach everyone?”.

“This is because the same relative change of each probability will have the same effect on the extinction probability”. I agree with this, but I wonder whether tail risk is the relevant metric. I think it is better to look into the expected value density of the cost-effectiveness of saving a life, accounting for indirect longterm effects as I did. I predict this expected value density to be higher for the 1st layers, which respect a lower severity, but are more likely to be requested. So, to equalise the marginal cost-effectiveness of additional investments across all layers, it may well be better to invest more in prevention than in response, and more in response than in resilience.

Maxipok is not ok?

My conclusion that saving lives in normal times is better to improve the longterm future than doing so in catastrophes is in contrast to Nick Bostrom’s maxipok rule:

Maximize the probability of an “OK outcome,” where an OK outcome is any outcome that avoids existential catastrophe.

I question the above as follows under my framework:

• The benefits of saving a life tend to infinity as the post-catastrophe population goes to 0, i.e. as one is increasingly confident it would cause human extinction.
• Yet, the PDF of the severity of the catastrophe (ratio between the pre- and post-catastrophe population) tends to 0 in that case.
• The 2 points above have opposing effects in terms of the expected value of saving a human life, and one cannot consider each of them in isolation because they are not independent.
• The 2 points are encapsulated in the expected value density of the benefits of saving a life, which I think tends to 0 under reasonable assumptions as the severity of the catastrophe increases.

I wonder which of the following heuristics is better to improve the longterm future. Maximising:

• The probability of nearterm human welfare not dropping to zero (roughly as in maxipok).
• Nearterm human welfare.
• Nearterm welfare (not only of humans, but all sentient beings, including animals and beings with artificial sentience).

Maxipok matches the 1st of these to the extent nearterm risk of human extinction is a good proxy for nearterm existential risk^[3], so I guess Nick would suggest the 1st of the above is the best heuristic. Nevertheless, it naively seems to me that the last one is broader:

• It depends on the whole distribution of welfare instead of just its left tail.
• It encompasses all sentient beings instead of just humans.

So a priori I would conclude maximising nearterm welfare is the best heuristic among the above. Accordingly, as a 1st approximation, I believe all interventions could be fairly assessed based on a single metric like the number of disability-adjusted life years (DALYs) averted per dollar, as calculated through a standard cost-effectiveness analysis^[4] (CEA). Ideally, cost-effectiveness analyses would account for effects on non-human beings too.

1. ^{^}

    Here is the relevant excerpt:

   For example, suppose one saved a drowning child 10,000 years ago, when the human population was estimated to be only in the millions. For convenience, we’ll posit a little over 7 million, 1/1000th of the current population. Since the child would add to population pressures on food supplies and disease risk, the effective population/economic boost could range from a fraction of a lifetime to a couple of lifetimes (via children), depending on the frequency of famine conditions. Famines were not annual and population fluctuated on a time scale of decades, so I will use 20 years of additional life expectancy.

   So, for ~ 20 years the ancient population would be 1/7,000,000th greater, and economic output/technological advance. We might cut this to 1/10,000,000 to reflect reduced availability of other inputs, although increasing returns could cut the other way. Using 1/10,000,000 cumulative world economic output would reach the same point ~ 1/500,000th of a year faster. An extra 1/500,000th of a year with around our current population of ~7 billion would amount to an additional ~14,000 life -years, 700 times the contemporary increase in life years lived. Moreover, those extra lives on average have a higher standard of living than their ancient counterparts.

   Readers familiar with Nick Bostrom’s paper on astronomical waste will see that this is a historical version of the same logic: when future populations will be far larger, expediting that process even slightly can affect the existence of many people. We cut off our analysis with current populations, but the greater the population this growth process will reach, the greater long-run impact of technological speedup from saving ancient lives.

2. ^{^}

    This is a decent goal in the model I presented previously if the post-catastrophe population is not too different from the pre-catastrophe one.

3. ^{^}

    Human extinction may not be an existential catastrophe if it is followed by the emergence of another intelligent species or caused by benevolent artificial intelligence.

4. ^{^}

    I prefer focusing on wellbeing-adjusted life years (WELLBYs) instead of DALYs, but both work for the point I am making as long as they are calculated through a standard CEA. Elliott Thornley and Carl Shulman argued longtermists should commit to acting in accordance with a catastrophe policy driven by standard cost-benefit analysis (CBA), but only in the political sphere, whereas I think the same holds in other contexts.

Owen Cotton-Barratt @ 2024-04-20T14:09 (+12)

I'm worried that modelling the tail risk here as a power law is doing a lot of work, since it's an assumption which makes the risk of very large events quite small (especially since you're taking a power law in the ratio, aside from the threshold from requiring a certain number of humans to have a viable population, the structure of the assumption essentially gives that extinction is impossible).

But we know from (the fancifully named) dragon king theory that the very largest events are often substantially larger than would be predicted by power law extrapolation.

Vasco Grilo @ 2024-04-20T22:03 (+2)

Thanks for the critique, Owen! I strongly upvoted it.

I'm worried that modelling the tail risk here as a power law is doing a lot of work, since it's an assumption which makes the risk of very large events quite small (especially since you're taking a power law in the ratio

Assuming the PDF of the ratio between the initial and final population follows a loguniform distribution (instead of a power law), the expected value density of the cost-effectiveness of saving a life would be constant, i.e. it would not depend on the severity of the catastrophe. However, I think assuming a loguniform distribution for the ratio between the initial and final population majorly overestimates tail risk. For example, I think a population loss (over my period length of 1 year^[1]) of 90 % to 99 % (ratio between the initial and final population of 10 to 100) is more likely than a population loss of 99.99 % to 99.999 % (ratio between the initial and final population of 10 k to 100 k), whereas a loguniform distribution would predict both of these to be equally likely.

aside from the threshold from requiring a certain number of humans to have a viable population

My reduction in population is supposed to refer to a period of 1 year, but the above only decreases population over longer horizons. 

the structure of the assumption essentially gives that extinction is impossible

I think human extinction over 1 year is extremely unlikely. I estimated 5.93*10^-12 for nuclear wars, 2.20*10^-14 for asteroids and comets, 3.38*10^-14 for supervolcanoes, a prior of 6.36*10^-14 for wars, and a prior of 4.35*10^-15 for terrorist attacks.

But we know from (the fancifully named) dragon king theory that the very largest events are often substantially larger than would be predicted by power law extrapolation.

Interesting! I did not know about that theory. On the other hand, there are counterexamples. David Roodman has argued the tail risk of solar storms decreases faster than predicted by a power law:

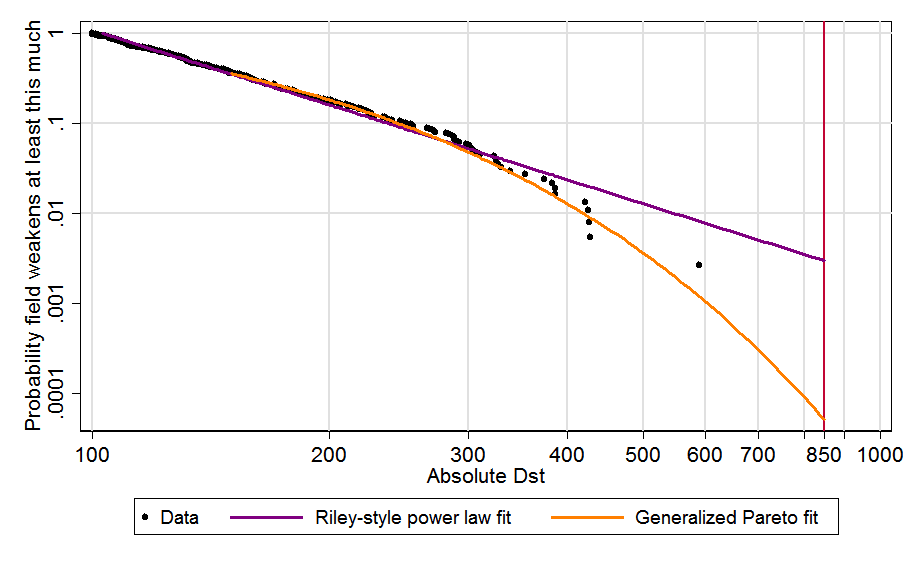
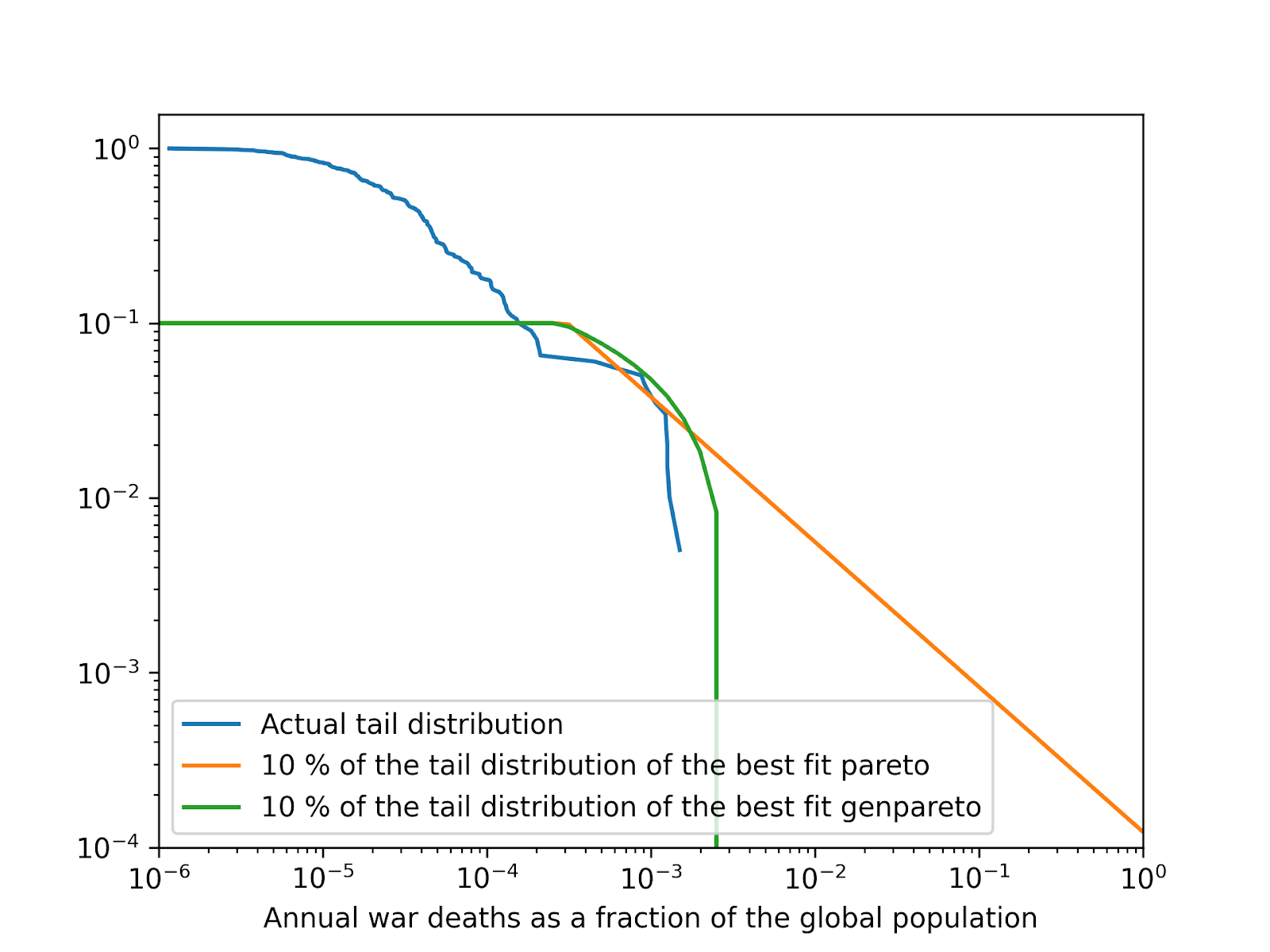
I have also found the tail risk of wars decreases faster than predicted by a power law:

Do you have a sense of the extent to which the dragon king theory applies in the context of deaths in catastrophes?

1. ^{^}

   I have now clarified this in the post.

Owen Cotton-Barratt @ 2024-04-20T22:45 (+5)

I think human extinction over 1 year is extremely unlikely. I estimated 5.93*10^-12 for nuclear wars, 2.20*10^-14 for asteroids and comets, 3.38*10^-14 for supervolcanoes, a prior of 6.36*10^-14 for wars, and a prior of 4.35*10^-15 for terrorist attacks.

Without having dug into them closely, these numbers don't seem crazy to me for the current state of the world. I think that the risk of human extinction over 1 year is almost all driven by some powerful new technology (with residues for the wilder astrophysical disasters, and the rise of some powerful ideology which somehow leads there). But this is an important class! In general dragon kings operate via something which is mechanically different than the more tame parts of the distribution, and "new technology" could totally facilitate that.

Do you have a sense of the extent to which the dragon king theory applies in the context of deaths in catastrophes?

Unfortunately, for the relevant part of the curve (catastrophes large enough to wipe out large fractions of the population) we have no data, so we'll be relying on theory. My understanding (based significantly just on the "mechanisms" section of that wikipedia page) is that dragon kings tend to arise in cases where there's a qualitatively different mechanism which causes the very large events but doesn't show up in the distribution of smaller events. In some cases we might not have such a mechanism, and in others we might. It certainly seems plausible to me when considering catastrophes (and this is enough to drive significant concern, because if we can't rule it out it's prudent to be concerned, and risk having wasted some resources if we turn out to be in a world where the total risk is extremely small), via the kind of mechanisms I allude to in the first half of this comment.

Vasco Grilo @ 2024-04-21T09:29 (+2)

I think that the risk of human extinction over 1 year is almost all driven by some powerful new technology (with residues for the wilder astrophysical disasters, and the rise of some powerful ideology which somehow leads there). But this is an important class! In general dragon kings operate via something which is mechanically different than the more tame parts of the distribution, and "new technology" could totally facilitate that.

To clarify, my estimates are supposed to account for unknown unknowns. Otherwise, they would be any orders of magnitude lower.

Unfortunately, for the relevant part of the curve (catastrophes large enough to wipe out large fractions of the population) we have no data, so we'll be relying on theory.

I found the "Unfortunately" funny!

My understanding (based significantly just on the "mechanisms" section of that wikipedia page) is that dragon kings tend to arise in cases where there's a qualitatively different mechanism which causes the very large events but doesn't show up in the distribution of smaller events. In some cases we might not have such a mechanism, and in others we might.

Makes sense. We may even have both cases in the same tail distribution. The tail distribution of the annual war deaths as a fraction of the global population is characteristic of a power law from 0.001 % to 0.01 %, then it seems to have a dragon king from around 0.01 % to 0.1 %, and then it decreases much faster than predicted by a power law. Since the tail distribution can decay slower and faster than a power law, I feel like this is still a decent assumption.

It certainly seems plausible to me when considering catastrophes (and this is enough to drive significant concern, because if we can't rule it out it's prudent to be concerned, and risk having wasted some resources if we turn out to be in a world where the total risk is extremely small), via the kind of mechanisms I allude to in the first half of this comment.

I agree we cannot rule out dragon kings (flatter sections of the tail distribution), but this is not enough for saving lives in catastrophes to be more valuable than in normal times. At least for the annual war deaths as a fraction of the global population, the tail distribution still ends up decaying faster than a power law despite the presence of a dragon king, so the expected value density of the cost-effectiveness of saving lives is still lower for larger wars (at least given my assumption that the cost to save a life does not vary with the severity of the catastrophe). I concluded the same holds for the famine deaths caused by the climatic effects of nuclear war.

One could argue we should not only put decent weight on the existence of dragon kings, but also on the possibility that they will make the expected value density of saving lives higher than in normal times. However, this would be assuming the conclusion.

Stan Pinsent @ 2024-04-22T07:54 (+11)

Using PDF rather than CDF to compare the cost-effectiveness of preventing events of different magnitudes here seems off.

You show that preventing (say) all potential wars next year with a death toll of 100 is 1000^1.6 = 63,000 times better in expectation than preventing all potential wars with a death toll of 100k.

More realistically, intervention A might decrease the probability of wars of magnitude 10-100 deaths and intervention B might decrease the probability of wars of magnitude 100,000 to 1,000,000 deaths. Suppose they decrease the probability of such wars over the next n years by the same amount. Which intervention is more valuable? We would use the same methodology as you did except we would use the CDF instead of the PDF. Intervention A would be only 1000^0.6 = 63 times as valuable.

As an intuition pump we might look at the distribution of military deaths in the 20th century. Should the League of Nations/UN have spent more effort preventing small wars and less effort preventing large ones?

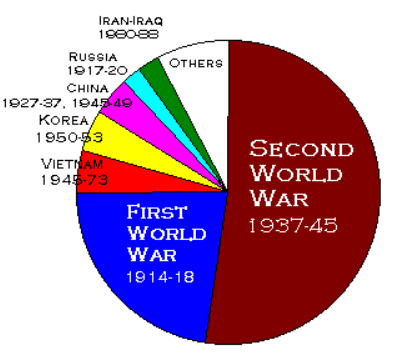
The data actually makes me think that even the 63x from above is too high. I would say that in the 20th century, great-power conflict > interstate conflict > intrastate conflict should have been the order of priorities (if we wish to reduce military deaths). When it comes to things that could be even deadlier than WWII, like nuclear war or a pandemic, it's obvious to me that the uncertainty about the death toll of such events increases at least linearly with the expected toll, and hence the "100-1000 vs 100k-1M" framing is superior to the PDF approach.

Vasco Grilo @ 2024-04-22T17:20 (+3)

Thanks for the comment, Stan!

Using PDF rather than CDF to compare the cost-effectiveness of preventing events of different magnitudes here seems off.

Technically speaking, the way I modelled the cost-effectiveness:

• I am not comparing the cost-effectiveness of preventing events of different magnitudes.
• Instead, I am comparing the cost-effectiveness of saving lives in periods of different population losses.

Using the CDF makes sense for the former, but the PDF is adequate for the latter.

You show that preventing (say) all potential wars next year with a death toll of 100 is 1000^1.6 = 63,000 times better in expectation than preventing all potential wars with a death toll of 100k.

I agree the above follows from using my tail index of 1.6. It is just worth noting that the wars have to involve exactly, not at least, 100 and 100 k deaths for the above to be correct.

More realistically, intervention A might decrease the probability of wars of magnitude 10-100 deaths and intervention B might decrease the probability of wars of magnitude 100,000 to 1,000,000 deaths. Suppose they decrease the probability of such wars over the next n years by the same amount. Which intervention is more valuable? We would use the same methodology as you did except we would use the CDF instead of the PDF. Intervention A would be only 1000^0.6 = 63 times as valuable.

This is not quite correct. The expected deaths from wars with $d_1$ to $d_2$ deaths is ${\int }_{d_1}^{d_2}x\frac{\alpha {d_m}^{\alpha }}{x^{\alpha +1}}dx=\frac{\alpha {d_m}^{\alpha }({m_1}^{1-\alpha }-{m_2}^{1-\alpha })}{\alpha -1}$, where ${d_m}^{\alpha }$ are the minimum war deaths. So, for a tail index of $\alpha =1.6$, intervention A would be 251 (= (10^-0.6 - 100^-0.6)/((10^5)^-0.6 - (10^6)^-0.6)) times as cost-effective as B. As the upper bounds of the severity ranges of A and B get increasingly close to their lower bounds, the cost-effectiveness of A tends to 63 k times that of B. In any case, the qualitative conclusion is the same. Preventing smaller wars averts more deaths in expectation assuming war deaths follow a power law.

As an intuition pump we might look at the distribution of military deaths in the 20th century. Should the League of Nations/UN have spent more effort preventing small wars and less effort preventing large ones?

I do not know. Instead of relying on past deaths alone, I would rather use cost-effectiveness analyses to figure out what is more cost-effective, as the Centre for Exploratory Altruism Research (CEARCH) does. I just think it is misleading to directly compare the scale of different events without accounting for their likelihood, as in the example from Founders Pledge’s report Philanthropy to the Right of Boom I mention in the post.

When it comes to things that could be even deadlier than WWII, like nuclear war or a pandemic, it's obvious to me that the uncertainty about the death toll of such events increases at least linearly with the expected toll, and hence the "100-1000 vs 100k-1M" framing is superior to the PDF approach.

I am also quite uncertain about the death toll of catastrophic events! I used the PDF to remain consistent which Founders Pledge's example, which compared discrete death tolls (not ranges).

Stan Pinsent @ 2024-04-23T16:34 (+3)

Thanks for the detailed response, Vasco! Apologies in advance that this reply is slightly rushed and scattershot.

I agree that you are right with the maths - it is 251x, not 63,000x.

• I am not comparing the cost-effectiveness of preventing events of different magnitudes.
• Instead, I am comparing the cost-effectiveness of saving lives in periods of different population losses.

OK, I did not really get this!

In your example on wars you say

• As a consequence, if the goal is minimising war deaths^[2], spending to save lives in wars 1 k times as deadly should be 0.00158 % (= (10^3)^(-1.6)) as large.

Can you give an example of what might count as "spending to save lives in wars 1k times as deadly" in this context? 

I am guessing it is spending money now on things that would save lives in very deadly wars. Something like building a nuclear bunker vs making a bullet proof vest? Thinking about the amounts we might be willing to spend on interventions that save lives in 100-death wars vs 100k-death wars, it intuitively feels like 251x is a way better multiplier than 63,000. So where am I going wrong?

When you are thinking about the PDF of $\frac{P_i}{P_f}$, are you forgetting that ∇$\frac{P_i}{P_f}$ is not proportional to ∇$P_f$? 

To give a toy example: suppose $P_i=100$. 

Then if $90<p_f<100$ we have  $1<\frac{P_i}{P_f}<1.11$

If $10<p_f<20$ we have  $5<\frac{P_i}{P_f}<10$

The "height of the PDF graph" will not capture these differences in width. This won't matter much for questions of 100 vs 100k deaths, but it might be relevant for near-existential mortality levels.

Vasco Grilo @ 2024-04-23T18:50 (+2)

Can you give an example of what might count as "spending to save lives in wars 1k times as deadly" in this context?

For example, if one was comparing wars involding 10 k or 10 M deaths, the latter would be more likely to involve multiple great power, in which case it would make more sense to improve relationships between NATO, China and Russia.

Thinking about the amounts we might be willing to spend on interventions that save lives in 100-death wars vs 100k-death wars, it intuitively feels like 251x is a way better multiplier than 63,000. So where am I going wrong?

You may be right! Interventions to decrease war deaths may be better conceptualised as preventing deaths within a given severity range, in which case I should not have interpreted lirerally the example in Founders Pledge’s report Philanthropy to the Right of Boom. In general, I think one has to rely on cost-effectiveness analyses to decide what to prioritise.

When you are thinking about the PDF of $\frac{P_i}{P_f}$, are you forgetting that ∇$\frac{P_i}{P_f}$ is not proportional to ∇$P_f$?

I am not sure I got the question. In my discussion of Founders Pledge's example about war deaths, I assumed the value of saving one life to be the same regardless of population size, because this is what they were doing). So I did not use the ratio between the initial and population.