Enhancing Mathematical Modeling with LLMs: Goals, Challenges, and Evaluations

By Ozzie Gooen @ 2024-10-28T21:37 (+9)

Introduction

Motivation

At QURI, we've been investing in developing and analyzing mathematical models, recently focusing on Squiggle AI, a system that leverages LLMs to generate models using the Squiggle language. We believe LLMs hold substantial potential for improving reasoning and are keen to explore how best to integrate them with mathematical modeling.

While recent attempts to automate narrow forecasts using LLMs have shown promise, mathematical models can offer far greater expressiveness and power. We're particularly interested in LLMs' ability to generate complex forecasts and explanations through formal modeling. However, the lack of clear evaluations or benchmarks for these models poses a challenge. This essay aims to dissect the key aspects of mathematical models and suggest ways they can be automated and evaluated effectively.

Reflections / Epistemic Status

This post summarizes roughly a week of focused thinking on mathematical modeling and LLMs, building on my work with Squiggle AI. While I'm confident in many details of what we want from mathematical models, I have more uncertainty about the broader categorization framework presented here.

The intersection of LLMs and mathematical modeling is a niche topic in our community, and I expect low engagement with this piece. However, this niche status means this area is neglected. More attention here, even by casual readers, could go a long way.

I used LLMs for help writing this post. This has resulted in a dryer writing style, but I think it made things more understandable. If people suggest prompts for preferred writing styles, I'd be interested in those for future pieces. 

Some Recent Related Posts

• My Current Claims and Cruxes on LLM Forecasting & Epistemics
• Squiggle AI: An Early Project at Automated Modeling
• The RAIN Framework for Informational Effectiveness

The Need for a Nuanced Understanding of Mathematical Models

Stakeholders often have varying perspectives on the value of mathematical models:

• Decision-makers may view them as adjustable tools for quick scenario analysis.
• Analysts might see models as means to demonstrate reasoning processes.
• Researchers could focus on computationally intensive models for precise parameter estimation.

These differing views highlight the necessity for a more nuanced understanding of what mathematical models can offer. Evaluating and optimizing mathematical models is akin to assessing written essays: there's no one-size-fits-all criterion. Essays can be informative, enjoyable, or stylistically innovative, and similarly, mathematical models have a variety of features and benefits.

To effectively evaluate and optimize models, it's beneficial to:

1. Identify Specific Features and Benefits: Break down the components that contribute to a model's value.
2. Prioritize: Determine which features are most important for your goals.
3. Focus Efforts: Work on enhancing one category at a time, or specific subsets, to improve overall quality.

By clarifying these aspects, we can develop a clearer sense of our objectives and the outcomes we aim to achieve with mathematical modeling.

Overview

We identify four unique features of mathematical models and six benefits derived from these features:

Features:

1. Accuracy: The ability of models to produce precise and reliable estimates.
2. Dimensionality: Handling multivariate parameters for more expressive models.
3. Interpretability: Making models understandable to facilitate trust and insight.
4. Customizability: Allowing users to adjust models to reflect their own assumptions.

Benefits:

1. Coverage: Organizing a large number of estimates, for easy estimation and viewing.
2. Modularity: Reusing model components across different applications.
3. Personalization: Tailoring models to individual users or scenarios.
4. Auditability: Enabling verification of model assumptions and processes.
5. Ancillary Discoveries: Uncovering additional insights during the modeling process, other than the final answer.
6. Privacy: Protecting sensitive information through customizable parameters.

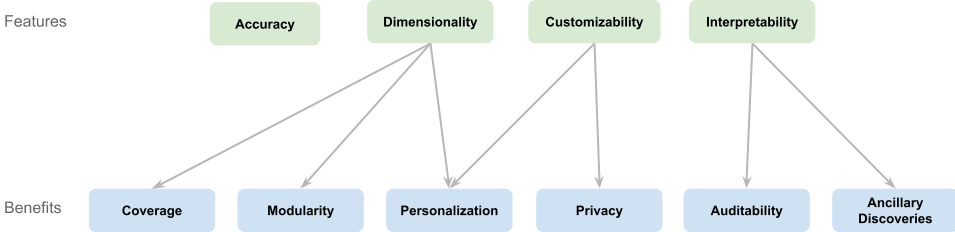
While these categories may overlap, they provide a framework for understanding and evaluating the multifaceted value of mathematical models. In practice, some features like accuracy are well-defined and can be isolated for evaluation, whereas others may need to be considered collectively.

Informal LLM Reasoning as a Baseline

Our primary interest lies in enhancing LLM systems that automate modeling. Currently, LLMs like ChatGPT and Claude generate responses using informal reasoning expressed in natural language, often producing surprisingly good estimates without formal code. For example, OpenAI's models can perform commendable Fermi estimates through direct queries.

This informal approach serves as a quality baseline. While it has the advantage of simplicity and speed, it also has limitations in complexity and precision. Formal mathematical modeling introduces additional complexity and cost, requiring more time to write and run models. Therefore, for formal models to be valuable, their benefits must outweigh these additional costs.

One challenge lies in discerning where formal modeling adds significant value over the baseline informal approach. There will be situations where the costs of modeling exceed the benefits, and others where clever modeling approaches offer substantial advantages. Over time this knowledge could be built into LLM systems that make smart assessments and build models of specific types in situations where they would be net-valuable.

Scope Limitations

To focus our efforts, we will concentrate on creating models with clear goals that require significant computational work when a user poses a query. Specifically, we do not address:

• Question Selection: Evaluating or modifying the questions themselves is beyond our current scope, even though it could enhance usefulness.
• Large World Models: While building extensive models with interconnected estimates is valuable, evaluating their quality requires separate investigation. This will likely require evaluating specific large-scale modeling strategies and implementations.
• Data Analysis: Automated data analysis is a vast field on its own. Our focus is on intuition-heavy models and judgmental forecasting rather than data-intensive methods.

Features

1. Accuracy

Accuracy refers to the degree to which a mathematical model's outputs align with real-world observations or true values. It involves producing estimates or predictions that are as close as possible to reality. Different types and complexities of mathematical models can yield varying levels of accuracy.

Arguably, accuracy is the most important feature/benefit in this document. This is especially true in more advanced LLM systems that could build very complex estimates with little human oversight.

When Is It Useful?

• Complex Problem Solving: In scenarios where intuition may fall short, such as intricate engineering calculations or advanced scientific research.
• Risk Assessment: When evaluating the probability and impact of uncertain events, accurate models can significantly aid in mitigation strategies.
• Optimization Tasks: In operations research or logistics, where precise calculations are necessary to optimize resources.

However, not all questions benefit equally from mathematical modeling in terms of accuracy. Many low-level assumptions or readily available statistics, like "What is the height of the Eiffel Tower?", may not see significant accuracy improvements through modeling. Currently, we have crude heuristics that suggest when mathematical models might enhance accuracy, but more work is needed to have a better understanding.

Challenges and Limitations

• Data Quality: Accurate modeling requires high-quality, relevant data, which may not always be available.
• Model Selection: Choosing the appropriate modeling strategy for a given problem is crucial and can be non-trivial.
• Uncertainty Handling: Accurately representing and quantifying uncertainty is challenging but essential for model reliability.
• Calibration: Ensuring the model's outputs are calibrated to real-world conditions often requires sophisticated techniques.

Unique Aspects

One unique aspect of accuracy is its objectivity. Unlike other features below that may be subjective or context-dependent, accuracy can often be measured directly by comparing model outputs to actual outcomes. This objectivity makes it easier to evaluate and optimize models for accuracy. Techniques like reinforcement learning could potentially be employed to enhance the ability of LLMs to produce accurate models in domains where objective measures are available.

Accurately can also be self-assessed to an extent. If a model incorporates a calibrated method for handling uncertainty, it can provide users with explicit indications of its expected accuracy. Comparing the uncertainty in an intuitive guess with that of a model can reveal improvements. Suppose an intuitive estimate is a normal distribution with a mean of 50 and a standard deviation of 30, whereas the model outputs a distribution with a mean of 46 and a standard deviation of 15. The reduced standard deviation suggests increased precision, indicating that the model may have enhanced the expected accuracy. This aspect can be used for aggregating or filtering models when they are generated.

2. Dimensionality (Multivariate Parameters)

Traditional judgmental forecasting often deals with univariate parameters, such as estimating the probability or distribution of a single variable. In contrast, multivariate models consider multiple variables simultaneously, providing a more expressive and comprehensive representation.

For example, instead of predicting just "What is the probability of event X?", a multivariate model might estimate "For any time T and company C, what will be the market cap?", expressed as a function that can be evaluated across different inputs.

While there has been serious scientific work on narrow-domain data analysis for multivariate forecasting, or simple judgmental techniques with LLMs for univariate forecasting, there’s been very little on using LLMs with little data for general-domain multivariate forecasting.

Benefits

• Expressiveness: Multivariate parameters allow models to capture complex relationships between variables, leading to richer insights.
• Coverage: They enable the organization and efficient calculation of large numbers of estimates.
• Modularity: Multivariate functions facilitate modular design in modeling, similar to how functions work in programming, allowing for components to be reused and combined in various ways.
• Personalization: By considering additional variables, models can produce estimates tailored to specific individuals or scenarios.

When Is It Useful?

• Complex Queries: There could be many situations where users will specifically request data that’s best expressed using multivariate estimates. It seems likely that these situations will typically involve one to three dimensions.
• Long-term Estimation Deliverables: High-dimension estimates could be useful in settings where some users want to provide others with complex forecasts. In these cases, these estimates could be used for highly-varied use cases. As such, these might use two to over twenty dimensions.
• Modular Forecasts: In the case where estimates are composed using formal programming, then some amount of dimensionality seems highly useful. There is still a great deal of uncertainty in understanding what heuristics will become common practice for this.

Challenges and Limitations

• Dimension selection: For any given question or problem, dimensions should be chosen that are useful for answering that. This includes setting up ontologies when tabular results are needed; for example, outlining a good list of interventions for a given organization.
• Interpretability: As model outputs become more complex, they can become harder to understand and explain. Visualizations can become prohibitively complex.
• Computational Complexity: Handling multiple variables increases the computational resources required.
• Data Requirements: Multivariate models often require more data to accurately estimate relationships between variables.

3. Interpretability

Interpretability is the degree to which a human can understand the internal mechanics of a model and the rationale behind its outputs. It encompasses the clarity and transparency with which the model's assumptions, processes, and results are presented.

For example, consider two people estimating the number of piano tuners in New York City. One says, "I think there are 5 to 20 piano tuners because it sounds right," while the other provides a detailed, step-by-step calculation. The latter is more interpretable because the reasoning is explicit and can be scrutinized.

Interpretability includes various features that aid understanding, such as visualizations, explanations, and sensitivity analyses. It covers ideas like reasoning transparency and epistemic legibility.

Importance

• Trust Building: Users are more likely to trust models when they understand how results are derived.
• Auditability: Interpretability allows stakeholders to question and investigate assumptions, especially when the modeler is not fully trusted.
• Knowledge Sharing: Transparent models facilitate the dissemination of insights and reasoning processes.
• Error Detection: Clear models make it easier to identify and correct mistakes or biases.

Challenges and Limitations

• Complexity vs. Simplicity: Highly detailed models may become cumbersome or overwhelming, while overly simplified models may omit crucial details.
• Complex Visualizations: Technically, it can be very difficult to make custom charts for different parameters. Existing plotting libraries often have significant limitations.
• Cherry-Picking: Models can be selectively presented to support a particular outcome, undermining transparency. This means that for a model to fully be interpretable, the modeling process itself (including information on the author) should be transparent.
• Varying Expertise Levels: Readers could have highly varying levels of expertise. It can be very difficult to provide explanations that will make sense for all of them.

4. Customizability

Customizability refers to the ability of users to modify a mathematical model's parameters or logic to reflect their own assumptions or preferences. This feature allows models to be adapted to different scenarios or individual viewpoints.

A common example is an Excel calculator provided to clients, where they can adjust input parameters and immediately see how changes affect the results.

Importance

• Empowerment: Users can take an active role in the modeling process, leading to greater engagement and ownership.
• Adaptability: Models can be quickly adjusted to accommodate new data, scenarios, or hypotheses without starting from scratch.
• Conflict Resolution: In situations where there is disagreement about key assumptions, customizability allows each party to explore outcomes based on their perspectives.

When Is It Useful?

• Decision-Making Processes: When users need to test various scenarios to inform choices.
• Personalized Outputs: In contexts where different users have unique needs or preferences.
• Sensitive Parameters: When certain assumptions are contentious or confidential, allowing users to input their values privately.

Challenges and Limitations

• Complexity Management: Allowing extensive customization can make models more complex and harder to maintain. Typically, only small subsets of parameters are made customizable.
• User Understanding: To meaningfully engage with a customizable model, users must deeply understand the customizable parameters. This could require a lot of sophistication and comprehension.
• User Error: Customizable estimates generally open estimates up to epistemic mistakes by users. Many might unknowingly provide poorly calibrated estimates, for example.

Benefits

1. Coverage

Coverage refers to a mathematical model's ability to address a wide range of variables, scenarios, or user needs by incorporating multivariate parameters. By moving beyond univariate estimates, models provide comprehensive information through a standardized interface, enhancing their utility across diverse requirements.

Importance

• Broad Applicability: Coverage enables models to be versatile tools usable by various users in different contexts.
• Efficiency for Analysts: Analysts can generate extensive sets of estimates with minimal additional effort.
• Enhanced Decision-Making: Comprehensive models offer decision-makers a fuller picture for more informed choices.

When Is It Useful?

• Large-Scale Forecasting: Organizations with significant resources focusing on important questions benefit from extensive coverage.
• Sophisticated Users and Tools: When users have the expertise and tools to handle complex models.
• Diverse Scenarios: Estimates needed for a wide variety of actors or circumstances require additional coverage.
• Generalization of Results: Analysts can efficiently extend estimates to more variables or time frames (e.g., forecasting GDP for multiple years).
• Complex Optimization: Critical for decisions involving optimization over multiple variables.

Challenges and Limitations

• Formal Ontologies Requirement: Models rely on predefined categories and struggle with arbitrary or unstructured data.
• Resource Intensiveness: Developing extensive coverage can be labor-intensive and may require sacrifices in quality or increased costs.

Distinction from Modularity

While Coverage focuses on what the model addresses—the breadth of variables and scenarios—it is distinct from Modularity, which deals with how the model is built through structural design of its components. Coverage enhances the model's scope and applicability, whereas componentization (formerly modularity) pertains to organizing the model into interchangeable parts for ease of development and maintenance.

2. Modularity

Modularity involves designing mathematical models as collections of discrete, self-contained components or functions that can be independently developed, tested, and reused. Similar to how modular programming builds complex software from individual functions, modularity in modeling enables the reuse of estimation functions across different models and contexts.

For example, an estimator might create a function that calculates the CO2 emissions of a flight based on specific inputs. Other analysts can then incorporate this function into their cost-benefit analyses without needing to recreate the underlying calculations.

Importance

• Reusability: Componentization allows established estimation functions to be reused, saving time and resources.
• Efficiency: By leveraging existing components, modelers can focus on higher-level analyses rather than redeveloping foundational elements.
• Consistency: Using common components promotes uniformity across different models and analyses.
• Collaboration: Facilitates sharing and collective improvement of models within a community or organization.

When Is It Useful?

• Trusted Components: When certain estimation functions are widely accepted as accurate and reliable, incorporating them enhances the credibility of new models. For instance, a charity estimating the impact of donations on bio-safety could import a respected estimate of the value of that cause.
• Complex Modeling: In building intricate models where standard components can simplify development and maintenance.

A practical vision for modularity includes developing a repository of commonly used estimation functions—perhaps 100 to 1,000—that Large Language Models (LLMs) can call upon when generating responses to future queries.

Challenges and Limitations

• Trust Issues: Analysts may be hesitant to use components developed by others due to concerns about accuracy or biases. For example, if Bob creates a complex model of air quality costs and Sophie doesn't trust it, she may avoid using his component.
• Integration Effort: Even if a component is trusted, the time required to understand and effectively integrate it can be a barrier.
• Technical Barriers: There are challenges in creating programming environments that make it easy to inspect, import, run, and update shared estimation functions, especially probabilistic ones.

These challenges can be partially addressed by:

• Establishing Trusted Platforms: Using forecasting platforms with incentives for accuracy can build trust in shared models.
• Developing User-Friendly Tools: Languages and environments like Squiggle are experimenting with ways to facilitate componentization.
• Community Standards: Encouraging the adoption of common standards and documentation practices to ease integration.

3. Personalization

Personalization involves tailoring models and estimates to account for individual differences or preferences. This can mean adjusting models based on specific details about a person, organization, or entity, or accommodating differing assumptions among users.

There are two main reasons for personalization:

1. Adjustment for Specific Details: For example, estimating the expected benefit of a medical intervention by considering a patient's biographical data.
2. Differing Assumptions: Users may have varying beliefs or opinions about key assumptions, such as the effectiveness of a political candidate, necessitating adjustments to the model.

When Is It Useful?

• Customized Solutions: In healthcare, finance, or education, where individual characteristics significantly impact outcomes.
• Disparate User Beliefs: When users hold different views on critical assumptions, personalization allows each to see results that align with their perspectives.

Adjustments based on specific details are often straightforward to implement, though they may require substantial work to gather and incorporate all the necessary data. Accommodating differing assumptions among users is more challenging, as it requires isolating and representing key epistemic disagreements.

4. Auditability

Auditability refers to the ease with which a model can be examined and verified by a third party to assess its trustworthiness and validity. It encompasses the transparency of the model's reasoning, assumptions, and processes.

Key aspects that facilitate auditability include:

• Clear reasoning and documentation.
• Disclosure of questionable assumptions.
• Transparency about the modeling process to avoid biases.
• External evaluations or validations by trusted third parties.
• Alignment with external data or consensus from other reputable sources.
• Knowledge of the model creator's incentives and bias.

Importance

• Building Trust: Auditability is crucial in establishing confidence among stakeholders, especially when the model's outcomes have significant implications.
• Accountability: Transparent models allow for accountability, ensuring that biases or errors can be identified and addressed.
• Regulatory Compliance: In certain industries, auditability is a legal requirement to ensure fairness and prevent malpractice.

When Is It Useful?

• High-Stakes Decisions: In areas like finance, healthcare, or policy-making, where decisions based on models have significant consequences.
• Differential Trust Scenarios: When some models or modelers are trusted more than others, auditability allows users to assess individual models on their merits.
• Regulated Industries: Where compliance standards require models to be auditable and transparent.

Sub-Benefits

• Quality Improvement: Auditing can identify areas for model enhancement, leading to better performance over time. This can be particularly useful for LLMs.

Auditability in LLM Systems

In the context of LLM systems, auditability takes on new dimensions. Automated epistemic processes in LLMs can potentially be more transparent than human reasoning, as all formal prompts and code logic can be audited and evaluated. While LLMs have internal biases, these might be systematically identified, tested, and mitigated.

5. Ancillary Discoveries

Ancillary Discoveries are additional insights or findings that emerge during the modeling process, which may be as valuable as or even more valuable than the primary results. These discoveries often relate to underlying patterns, relationships, or critical factors that were not the initial focus of the model.

There are different forms of ancillary discovery:

1. Human Readers: Individuals reviewing the model may glean insights beyond the immediate results.
2. Iterative Modeling: Humans or LLMs can use insights from one modeling attempt to refine subsequent models on the same question.
3. LLM Readers for Formal Knowledge Building: LLMs can analyze models across various subjects to extract critical ideas, adding them to a knowledge base.
4. LLM Training: If future LLMs are trained directly on models, then any intermediate discoveries that are found would be captured by the training process.

Importance

• Deepened Understanding: Ancillary discoveries contribute to a more profound understanding of the system or problem being modeled.
• Efficiency Gains: Insights gained from some models can be used for future models.

One approach to maximizing ancillary discoveries is to have LLMs explicitly search for and articulate them. For example, after generating a model, an LLM could be prompted to identify any additional insights that could inform future models.

Challenges and Limitations

• Diminishing Returns: The value of ancillary discoveries may decrease over time as critical lessons are learned and documented.
• Uncertainty of Value: Not all ancillary findings will be useful or relevant, making it hard to predict their impact.

It's also unclear how effectively LLMs can leverage ancillary knowledge from regular modeling outside of standard training or distillation processes.

6. Privacy

Privacy in the context of mathematical modeling refers to the protection of sensitive information, ensuring that users or decision-makers do not have to reveal their private data or viewpoints to those conducting the analysis. One traditional problem in decision-relevant modeling is that key decision-makers may be reluctant to disclose their true beliefs or confidential data due to concerns about confidentiality. Customizable models address this issue by allowing users to adjust estimates without revealing their inputs to the modelers.

Importance

• Confidentiality: Protects sensitive information, which may be critical in competitive industries or when dealing with personal data.
• Compliance: Helps meet legal and regulatory requirements related to data protection and privacy.

When Is It Useful?

• Sensitive Domains: In political, medical, or financial contexts where data is highly confidential.
• Untrusted Environments: When the modeling process is not fully trusted to be secure or confidential.
• Third-Party Services: Users may not want to share sensitive information with LLM providers or external analysts.

For example, a policymaker might not want to disclose their personal valuation of human life to an AI service provider but still needs to use models that incorporate this parameter.

LLMs vs. Humans

When models are created by human analysts and provided to decision-makers, those decision-makers might be hesitant to share their true information due to privacy concerns. In these cases, customizability becomes essential for guaranteeing privacy. It allows decision-makers to adjust key parameters themselves without revealing sensitive data to the modelers.

Large Language Models (LLMs) introduce different considerations. LLM solutions that report data back to large companies like OpenAI or Google might offer less privacy than working directly with a trusted human analyst, as sensitive information could be transmitted or stored externally. However, LLM solutions that utilize locally hosted models can provide significantly greater privacy. In these cases, all data processing occurs on the user's own infrastructure, ensuring that sensitive information is not transmitted to external servers.

In scenarios where locally hosted LLMs are used, model adjustability might not be as critical for maintaining privacy because the data never leaves the secure environment. Instead, the focus shifts to the hosting details of the LLM solution. Ensuring that the LLM is deployed in a secure, private environment becomes paramount for maintaining confidentiality. Thus, while customizability remains valuable, the primary concern for privacy with LLMs is how and where the models are hosted and executed.

Key Takeaways

Item Summaries

Accuracy
Model accuracy should be evaluated and optimized under domains with clear answers. This is clearly both important and tractable. It's less clear how these results will generalize to domains with unclear answers; more work is needed here.

Coverage
It seems straightforward and important to evaluate the accuracy of models that output multivariate estimates. It's much harder, but perhaps less important, to evaluate the selection of specific dimensions and ontologies.

Modularity
Modularity probably doesn't need to be evaluated directly. However, modularity will likely be essential for creating large world models. These models might need separate methods of measurement and evaluation.

Personalization
Key aspects of personalization can be understood and optimized similar to coverage, but using person-specific topics.

Auditability
Auditability might be important early in the LLM automation process, when people and LLMs can't tell how good specific models are. The other key reason for it might be to oversee potentially unaligned AI systems. On the downside, auditability will likely be difficult to evaluate.

Ancillary Discoveries
Ancillary discoveries could be crucial early on, as they can represent valuable training data for future LLMs. Over time, critical lessons will be learned and documented, leading to decreased importance.

Privacy
LLMs can produce more private results than humans can. Because of this, the main challenge might be to ensure that the LLMs themselves are run on servers that maintain confidentiality. This requires less evaluation focus.

Formal Evaluations

Accuracy, coverage, and personalization can be formally evaluated together in domains with clear answers. Auditability might be the next aspect to which strict measurements can be applied; at the very least, LLMs could grade models.

Customizability, componentization, and ancillary discoveries might be optimized for certain applications based on user feedback and large-scale optimizations. Privacy issues in LLMs and models might reduce to standard LLM privacy concerns, potentially requiring no extra investigation or optimization.

It's important to remember that some characteristics aren't easily amenable to strict evaluations. For instance, many web applications like Google Docs or Perplexity include numerous small optimizations across various dimensions that assist users in ways difficult to measure or predict in advance. Quantitative models are likely similar. While formal estimation and optimization are possible for some narrow aspects of accuracy, coverage, and interpretability, many useful features and details will probably require extensive interaction with users. This is particularly true for front-end interfaces and other components that users engage with directly.

Conclusion

The integration of large language models (LLMs) with mathematical modeling presents an important opportunity to enhance reasoning, forecasting, and decision-making across various fields. By dissecting the key features—accuracy, coverage, modularity, personalization, interpretability, customizability, auditability, ancillary discoveries, and privacy—we gain a comprehensive understanding of how each contributes uniquely to the utility and effectiveness of mathematical models. These features offer significant benefits while also posing specific challenges that require thoughtful consideration.