An in-progress experiment to test how Laplace’s rule of succession performs in practice.

By NunoSempere @ 2023-01-30T17:41 (+57)

Note: Of reduced interest to generalist audiences.

Summary

I compiled a dataset of 206 mathematical conjectures together with the years in which they were posited. Then in a few years, I intend to check whether the probabilities implied by Laplace’s rule—which only depends on the number of years passed since a conjecture was created—are about right.

In a few years, I think this will shed some light on whether Laplace’s rule of succession is useful in practice. For people wanting answers more quickly, I also outline some further work which could be done to obtain results now. 

The dataset I’m using can be seen here (a). 

Probability that a conjecture will be resolved by a given year according to Laplace’s law.

I estimate the probability that a randomly chosen conjecture will be solved as follows:

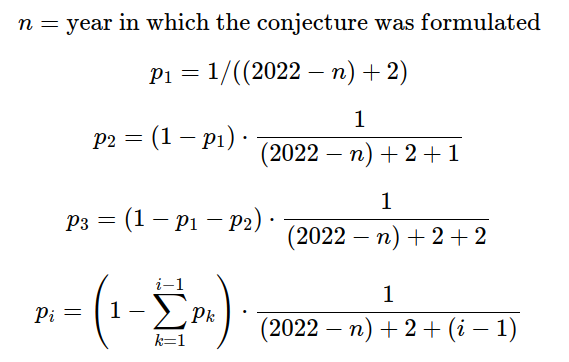
That is, the probability that the conjecture will first be solved in the year n is the probability given by Laplace conditional on it not having been solved any year before.

For reference, a “pseudo-count” corresponds to either changing the numerator to an integer higher than one, or to making n higher. This can be used to capture some of the structure that a problem manifests. E.g., if we don’t think that the prior probability of a theorem being solved in the first year is around 50%, this can be addressed by adding pseudo-counts. 

Code to do these operations in the programming language R can be found here. A dataset that includes these probabilities can be seen here.

Expected distribution of the number of resolved conjectures according to Laplace’s rule of succession

Using the above probabilities, we can, through sampling, estimate the number of conjectures in our database that will be solved in the next 3, 5, or 10 years. The code to do this is in the same R file linked a paragraph ago.

For three years

If we calculate the 90% and the 98% confidence intervals, these are respectively (6 to 16) and (4 to 18) problems solved in the next three years.

For five years

If we calculate the 90% and the 98% confidence intervals, these are respectively (11 to 24) and (9 to 27) problems solved in the next five years.

For ten years

If we calculate the 90% and the 98% confidence intervals, these are respectively (23 to 40) and (20 to 43) problems solved in the next five years.

Ideas for further work

Do this experiment for other topics besides mathematical theorems and for other methods besides Laplace’s law

Although I expect that this experiment restricted to mathematical experiments will already be decently informative, it would also be interesting to look at the performance of Laplace’s law for a range of topics.

It might also be worth it to look at other approaches. In particular, I’d be interested in seeing the same experiment but for “semi-informative priors”—there is no particular reasons why that approach only has to apply to super-speculative areas like AI. So an experiment could look at experts trying to come up with semi-informative priors for events that are testable in the next few years, and this might shed some light into the general method.

Checking whether the predictions from Laplace’s law come true

In three, five, and ten years I’ll check the number of conjectures which have been resolved. If that falls outside the 99% confidence interval, I will become more skeptical of using Laplace’s law for arbitrary domains. I’ll then investigate whether Laplace’s law could be rescued in some way, e.g., by using its time-invariant version, by adding some pseudo-counts, or through some other method.

With pseudo-counts, the idea would be that there would be a number of unique pseudo-counts which would make Laplace output the correct probability in three years. Then the question would be whether that number of pseudo-counts is enough to make good predictions about the five- and ten-year periods.

Comparison against prediction markets

I’d also be curious about posting these conjectures to Manifold Markets or Metaculus and seeing if these platforms can outperform Laplace’s law.

Using an older version of the Wikipedia entry to come up with answers now

If someone was interested in resolving the question sooner without having to wait, one could redo this investigation but:

1. Look at the List of unsolved problems in mathematics from 2015,
2. checking to see how many have been resolved since then
3. check whether adding pseudo-counts to fit the number of theorems solved by 2018 is predictive of how many problems have been solved by 2022

The reason why I didn’t do this myself is that step 2. would be fairly time intensive, and I was pretty fed up after creating the dataset as outlined in the appendix.

Acknowledgements

This is a project of the Quantified Uncertainty Research Institute (QURI). Thanks to Ozzie Gooen and Nics Olayres for giving comments and suggestions. 

PS: You can subscribe to QURI's posts here, or to my own blog posts here.

Appendix: Notes on the creation of the dataset

I went through the list of conjectures on this Wikipedia page: List of unsolved problems in mathematics (a) and filtered them as follows:

1. Ignored additional lists
2. Ignore conjectures which have already been solved
3. In cases where the date in which the conjecture was made, approximate it
4. Ignore theorems without a full Wikipedia page or a large enough section in another page, as this would have made tracking down the date or tracking down resolution too difficult
5. Ignoring the “Combinatorial games” section, as well as the many prime conjectures, as most were too short
6. For problems that are equivalent, take the oldest formulation
7. I sometimes ignored the case where a conjecture had been proven, and this led to even more conjectures

Note that if it turns out that a given conjecture was already solved by November 2022, it should be excluded from the dataset, rather than counted as a positive