quila's Quick takes

a moral intuition i have: to avoid culturally/conformistly-motivated cognition, it's useful to ask:

if we were starting over, new to the world but with all the technology we have now, would we recreate this practice?

example: we start and out and there's us, and these innocent fluffy creatures that can't talk to us, but they can be our friends. we're just learning about them for the first time. would we, at some point, spontaneously choose to kill them and eat their bodies, despite us having plant-based foods, supplements, vegan-assuming nutrition guides, etc? to me, the answer seems obviously not. the idea would not even cross our minds.

(i encourage picking other topics and seeing how this applies)

What is malevolence? On the nature, measurement, and distribution of dark traits was posted two weeks ago (and i recommend it). there was a questionnaire discussed in that post which tries to measure the levels of 'dark traits' in the respondent.

i'm curious about the results^[1] of EAs^[2] on that questionnaire, if anyone wants to volunteer theirs. there are short and long versions (16 and 70 questions).

1. ^{^}

   (or responses to the questions themselves)

2. ^{^}

   i also posted the same quick take to LessWrong, asking about rationalists

Are your values about the world, or the effects of your actions on the world?

An agent who values the world will want to effect the world, of course. These have no difference in effect if they're both linear, but if they're concave...

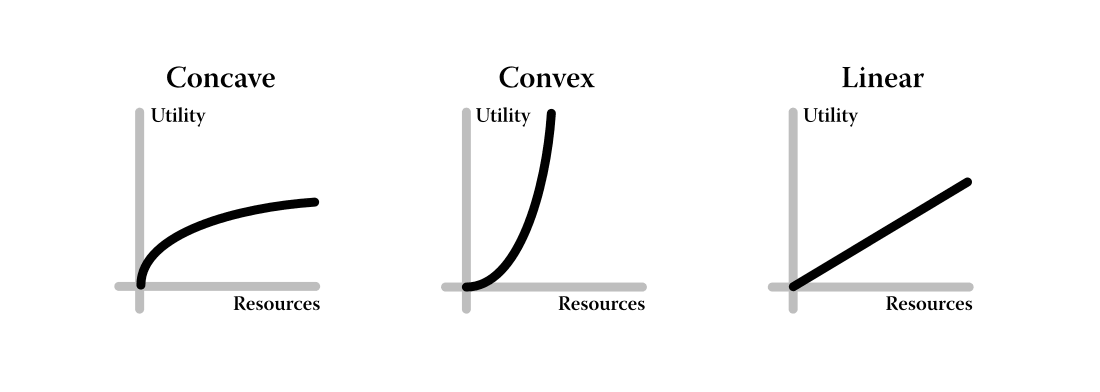
Then there is a difference.^[1]

If an agent has a concave value function which they use to pick each individual action: $\sqrt{L}$ where L is the amount of lives saved by the action, then that agent would prefer a 90% chance of saving 1 life (for √1 × .9 = .9 utility), over a 50% chance of saving 3 lives (for √3 × .5 = .87 utility). The agent would have this preference each time they were offered the choice.

This would be odd to me, partly because it would imply that if they were presented this choice enough times, they will appear to overall prefer an x% chance at saving n lives to an x% chance of saving >n lives. (Or rather, the probability distribution version instead of discrete version of that statement)

For example, after taking the first option 10 times, the probability distribution over amount of lives saved looks like this (on the left side). If they had instead took the second option 10 times, it would look like this (right side)

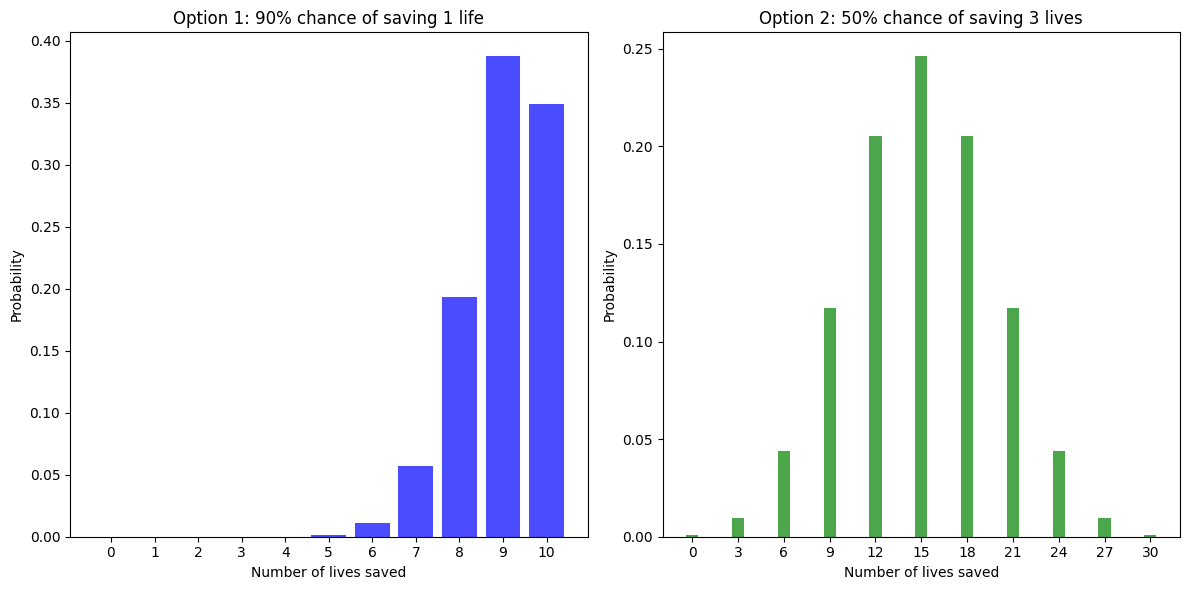
(Note: Claude 3.5 Sonnet wrote the code to display this and to calculate the expected utility, so I'm not certain it's correct. Calculation output and code in footnote^[2])

Now if we prompted the agent to choose between each of these probability distributions, they would assign an average utility of 3.00 to the one on the left, and 3.82 to the one on the right, which from the outside looks like contradicting their earlier sequence of choices.^[3]

We can generalize this beyond this example to say that, in situations like this, the agent's best action is to precommit to take the second option repeatedly.^[4]

We can also generalize further and say that for an agent with a concave function used to pick individual actions, the initial action which scores the highest would be to self-modify into (or commit to taking the actions of) an agent with a concave utility function over the contents of the world proper.^[5]

I wrote this after having a discussion (starts ~here at the second quote) with someone who seemed to endorse following concave utility functions over the possible effects of individual actions.^[6] I think they were drawn to this as a formalization of 'risk aversion', though, so I'd guess that if they find the content of this text true, they'd want to continue acting in a risk-averse-feeling way, but may search for a different formalization.

My motive for writing this though was mostly intrigue. I wasn't expecting someone to have a value function like that, and I wanted to see if others would too. I wondered if I might have just been mind-projecting this whole time, and if actually this might be common in others, and if that might help explain certain kinds of 'risk averse' behavior that I would consider suboptimal at fulfilling one's actual values^[7] (this is discussed more extensively in my linked comment).

1. ^{^}

   Image from 'All About Concave and Convex Agents'.

   For discussion of the actual values of some humans, I recommend 'Value Theory'

2. ^{^}

   Calculation for Option 1:
   Lives  Probability  Utility Prob * Utility
   ------------------------------------------
       0       0.0000   0.0000         0.0000
       1       0.0000   1.0000         0.0000
       2       0.0000   1.4142         0.0000
       3       0.0000   1.7321         0.0000
       4       0.0001   2.0000         0.0003
       5       0.0015   2.2361         0.0033
       6       0.0112   2.4495         0.0273
       7       0.0574   2.6458         0.1519
       8       0.1937   2.8284         0.5479
       9       0.3874   3.0000         1.1623
      10       0.3487   3.1623         1.1026
   ------------------------------------------
       Total expected utility:         2.9956
   
   Calculation for Option 2:
   Lives  Probability  Utility Prob * Utility
   ------------------------------------------
       0       0.0010   0.0000         0.0000
       3       0.0098   1.7321         0.0169
       6       0.0439   2.4495         0.1076
       9       0.1172   3.0000         0.3516
      12       0.2051   3.4641         0.7104
      15       0.2461   3.8730         0.9531
      18       0.2051   4.2426         0.8701
      21       0.1172   4.5826         0.5370
      24       0.0439   4.8990         0.2153
      27       0.0098   5.1962         0.0507
      30       0.0010   5.4772         0.0053
   ------------------------------------------
       Total expected utility:         3.8181

   code: 

   import numpy as np
   import matplotlib.pyplot as plt
   from scipy.stats import binom
   
   def calculate_utility(lives_saved):
       return np.sqrt(lives_saved)
   
   def plot_distribution(prob_success, lives_saved, n_choices, option_name):
       x = np.arange(n_choices + 1) * lives_saved
       y = binom.pmf(np.arange(n_choices + 1), n_choices, prob_success)
       
       bars = plt.bar(x, y, alpha=0.8, label=option_name)
       plt.xlabel('Number of lives saved')
       plt.ylabel('Probability')
       plt.title(f'Probability Distribution for {option_name}')
       plt.xticks(x)
       plt.legend()
       
       for bar in bars:
           height = bar.get_height()
           plt.text(bar.get_x() + bar.get_width()/2., height/2,
                    f'{height:.2%}',  # Changed to percentage format
                    ha='center', va='center', rotation=90, color='white')
   
   def calculate_and_print_details(prob_success, lives_saved, n_choices, option_name):
       x = np.arange(n_choices + 1) * lives_saved
       p = binom.pmf(np.arange(n_choices + 1), n_choices, prob_success)
       
       print(f"\nDetailed calculation for {option_name}:")
       print(f"{'Lives':>5} {'Probability':>12} {'Utility':>8} {'Prob * Utility':>14}")
       print("-" * 42)
       
       total_utility = 0
       for lives, prob in zip(x, p):
           utility = calculate_utility(lives)
           weighted_utility = prob * utility
           total_utility += weighted_utility
           print(f"{lives:5d} {prob:12.4f} {utility:8.4f} {weighted_utility:14.4f}")
       
       print("-" * 42)
       print(f"{'Total expected utility:':>27} {total_utility:14.4f}")
       
       return total_utility
   
   # Parameters
   n_choices = 10
   prob_1, lives_1 = 0.9, 1
   prob_2, lives_2 = 0.5, 3
   
   # Calculate and print details
   print("Calculation for Option 1:")
   eu_1 = calculate_and_print_details(prob_1, lives_1, n_choices, "Option 1")
   print("\nCalculation for Option 2:")
   eu_2 = calculate_and_print_details(prob_2, lives_2, n_choices, "Option 2")
   
   # Plot distributions
   plt.figure(figsize=(15, 6))
   
   plt.subplot(1, 2, 1)
   plot_distribution(prob_1, lives_1, n_choices, "Option 1 (90% chance of 1 life)")
   plt.subplot(1, 2, 2)
   plot_distribution(prob_2, lives_2, n_choices, "Option 2 (50% chance of 3 lives)")
   
   plt.tight_layout()
   plt.show()
   
   print(f"\nFinal Results:")
   print(f"Expected utility for Option 1: {eu_1:.4f}")
   print(f"Expected utility for Option 2: {eu_2:.4f}")

3. ^{^}

   (of course, if it happened it wouldn't really be a contradiction, it would just be a program being run according to what it says)

4. ^{^}

   (Though, if one accepts that, I have a nascent intuition that the same logic forces one to accept what I was writing about Kelly betting in the discussion this came from.)

5. ^{^}

   Recall that actions are picked only individually, not according to the utility the current function would assign to future choices made under the new utility function.

   (That would instead have its own exploits, namely looping between many small positive actions and one big negative 'undoing' action whose negative utility is square-rooted)

6. ^{^}

   (I initially thought they meant over the total effects of all their actions throughout their past and future, rather than per action.)

7. ^{^}

   I'll claim that if one doesn't reflectively endorse optimally fulfilling some values, then those are not their actual values, but maybe are a simplified version of them.