Shallow Report on Nuclear War (Arsenal Limitation)

By Joel Tan🔸 @ 2023-02-21T04:57 (+44)

Note: This report was produced with only one week of desktop research, for the purpose of identifying promising causes to evaluate at depth. We only have low confidence in our findings here, and the conclusions should generally be taken by readers as merely suggestive rather determinative.

Summary

Considering the expected benefits of eliminating the risk of nuclear war (i.e. averting nuclear war fatalities, averting nuclear war injuries, and consequently greater economic output), the expected costs (i.e. more conventional war fatalities, more conventional war injuries, and hence decreased economic output), as well as the tractability of lobbying for arsenal limitation, I find that the marginal expected value of lobbying for arsenal limitation to mitigate nuclear war to be 3,341,695 DALYs per USD 100,000, which is around 5000x as cost-effective as giving to a GiveWell top charity (CEA).

Key Points

• Importance: This is a strongly important cause, with 3.88 * 10¹⁰ DALYs at stake from now to the indefinite future. The expected benefits totally swamp the expected costs (with the latter being <0.001% of the former), and overall, around 81% of the burden is health related, while 19% is economic in nature.
• Neglectedness: There is a high degree of uncertainty, but it appears that the global stockpile of nuclear weapons is not declining in the long-term, especially if you factor in likely Chinese buildup, and current efforts do seem inadequate.
• Tractability: A moderately tractable solution is available, in the form of policy advocacy for nuclear arms limitation – which for the US and Russia means reducing current stockpiles, and which for the Chinese means forswearing planned increases.

Caveats

• This report was produced with only one week of research, and critically, only desktop research was used, without experts consulted due to the lack of time. More research – at the intermediate stage and subsequently deep stage – will be needed before we can have high confidence in these findings.
• The headline cost-effectiveness will almost certainly fall if this cause area is subjected to deeper research: (a) this is empirically the case, from past experience; and (b) theoretically, we suffer from optimizer's curse (where causes appear better than the mean partly because they are genuinely more cost-effective but also partly because of random error favouring them, and when deeper research fixes the latter, the estimated cost-effectiveness falls). As it happens, CEARCH intends to perform deeper research in this area, given that the headline cost-effectiveness meets our threshold of 10x that of a GiveWell top charity.

Further Discussion

• Results are very different from CEARCH's previous cost-effectiveness analysis and report on nuclear war, which looked at full abolishment as a solution and found a marginal expected value of 248 DALYS per USD 100,000 spent (i.e. 40% as cost-effective as GiveWell). The drastic increase in cost-effectiveness is driven by nuclear arms limitation being far more tractable than abolishment – which makes sense, since the USSR/Russia have signed numerous arms limitation treaties before, while abolishment has never happened outside of unique and unreplicable circumstances (i.e. post-Soviet and post-apartheid disarmament). Note that the increase in cost-effectiveness has nothing to do with a change in the assessed size of the problem – in fact, our estimate of the total net benefit of denuclearization has declined by a magnitude), as we've calibrated our analysis with perhaps more accurate estimates of the probability of nuclear war and of more precise instrumental discount rates for future harms. For more details on changes, refer to the changelog section below.
• Philosophically, we take the more conservative person-affecting view, in looking specifically at the welfare of actual people, whether present or future – as opposed to contingent/merely potential people that would not exist if not for our intervention (or lack thereof).
  • Under the totalist view, this cause area would naturally be even more cost-effective – roughly 6.4x more, insofar as any person saved now will have children, who will go on to have children too and so on, such that (given expected future birth and death rates, plus relevant discount rates) counterfactually 6.4 lives are created/maintained by the averting of one death.
  • That said, this may not matter too much, insofar as the same 6.4x multiplier applies to any cause area, not just existential risk causes – indeed, saving a poor person from malaria today would counterfactually be far more valuable than saving someone from nuclear war 100 years later, since birth rates are higher now.
  • Implicit in this extended analysis is the idea that birth rate is largely invariant to overall population size, such that there is no "bounceback effect" from near-extinction events (i.e. people will not have systematically more children after a devastating nuclear war, with the result that the overall human population takes a permanent level reduction); if this were not true, then saving lives from near-existential catastrophe would be more valuable than saving lives in the ordinary course of events. CEARCH intends to conduct more research on this issue, as this is critical to assessing the relative cost-effectiveness of existential risk vs non-existential risk cause areas.
• The results potentially overestimate the risks insofar as we focus on the three major nuclear war risks (i.e. NATO-Russia, US-China and India-Pakistan), and leave off the more minor flash points (e.g. NK-US, Iran-Israel) when calculating the average deaths from nuclear war.
• On the other hand, the results may also potentially underestimate the risks insofar as existing evaluations of the probability of nuclear war, which this analysis relies on, likely over-anchor on major conflicts and neglect the additional risks from more minor ones. This effect balances out the first issue, but to what extent, it is hard to say.
• Intuitively, my sense is that our estimates of the probability of advocacy success is still too optimistic, potentially by up to a magnitude. It would be valuable to consult experts on tractability – especially country-specific national security experts – if deeper research is done.
• There is also considerable uncertainty on the cost of advocacy, both in terms of the per annum cost and on how long it will take to succeed.
• That said, results are robust, insofar as the low-confidence tractability estimates can drop by three whole magnitudes and still leave the intervention to be comfortably more cost-effective than GiveWell.

Changelog

• Recalibrated estimates of the direct violent deaths from nuclear war (e.g. relooking assumptions, re-assessing study quality, fixing errors).
• Recalibrated the reversal rate by looking at the rate at which nuclear arms control treaties agreed to and put into effect by the US & Russia have been abrogated
• Recalibrated the growth/decline of the problem by looking at nuclear weapons stockpiles growth, population growth, and population ageing. 
• Reassessed the probability of full-blown nuclear war – the updated figure is more conservative, distinguishing as it does tactical nuclear attacks vs strategic vs full-blown nuclear war.
• Minor recalibration of the moral weights of the typical injury in either nuclear or conventional war
• Updated the approach to calculating the number of injuries from nuclear war
• Incorporated the economic effects of nuclear war and conventional war
• Updated the approach to calculating the number of fatalities from conventional war
• Updated the approach to calculating the number of injuries from conventional war
• Modelled the intervention of advocacy for US/Russia/China to reduce nuclear stockpiles to current Chinese levels, and in the process updating both the analysis of advocacy success and the expected costing.

Expected Benefit: Averting Nuclear War Fatalities

The first and primary benefit of eliminating the risk of nuclear war would be averting the nuclear war fatalities that would otherwise occur. Overall, around 3.13 * 10¹⁰ DALYs are at stake here, with this benefit modelled in the following way.

Moral Weights: I take the value of averting one death to be 29.3 DALYs. This is calculated as a function of (a) a human's full healthy life expectancy of 63.69; (b) a minor age-based philosophical discount; (c) assuming we save someone of the median age; (d) assuming that the median age is at the halfway mark to average age of death and that DALYs are equally distributed across age groups; and (e) a probability adjustment based on age distributions. For more details, refer to CEARCH's evaluative framework.

Scale: For the scale of the problem, we have to look at both the direct violent deaths from nuclear war as well as the indirect famine deaths from nuclear winter.

For direct violent deaths, I look at the three potential nuclear wars – NATO-Russia, US-China & India-Pakistan – since these have the highest expected harm.

• NATO/Russia nuclear war: For direct violent deaths from NATO-Russia nuclear war, I look at three different estimates. (a) First, there is the Rodriguez estimate, according to which we can expect 51 million deaths from nuclear attacks on military and civilian targets in the event of NATO-Russia nuclear war. (b) Second, there is the Wellerstein et al estimate, of 34.1 million deaths. Third, there is (c) the Toon, Robock & Turco estimate, of 100 million deaths, in the specific case of Russia targeting 1000 weapons on the US while the US retaliates with 1100 weapons on Russia. In aggregating these different estimates, I note the following points. (a) In Rodriguez's estimate, the probability distribution of countervalue targeting occuring – and hence the mean probability thereof – does not seem well-grounded; it would hence be best to only lightly weigh this estimate when aggregating multiple fatality estimates. (b) Meanwhile, the Wellerstein et al estimate relies on a plausible initial escalation from conventional to nuclear war but increasingly implausible escalation steps to full-scale nuclear conflict. (c) Finally, the Toon, Robock & Turco estimate does not factor in the possibility of counterforce targeting at all. Given these flaws, I ultimately end up using equal weightage, yielding an aggregate estimate of 61.7 million violent deaths from NATO-Russia nuclear war.
• US-China nuclear war: For direct violent deaths from US-China nuclear war, I again look at three different estimates. (a) First, there is the Kristensen, Norris & McKinzie estimate, of 21 million deaths; this looks specifically at the maximalist US-on-China counterforce scenario (since the US will want to eliminate all Chinese nuclear weapons to minimize retaliation, in the event the US decides to go nuclear at all), even while taking an average with respect to the number of potential retaliatory missile strikes in the Chinese countervalue response. (b) Second, there is the Toon, Robock & Turco estimate, of 225 million deaths; this considers a 1,100 warheads US attack on China and 1000 warhead Chinese attack on the US, given the projected Chinese arsenal by 2030. (c) Third, there is the Joint Chiefs of Staff 1961 estimate, which when extrapolated yields 207 million deaths; this averages the full force and alert force casualties for both urban and rural China, and then applies it to current Chinese population data, before adjusting by the Wellerstein et al fatality-to-casualty ratio; we add US casualties by scaling total (US & China) population against baseline Chinese population. In aggregating these different estimates, I note the following points. (a) Kristensen, Norris & McKinzie consider an implausibly low number of deployed Chinese countervalue nuclear missiles (and correspondingly also underestimate the necessary US counterforce attack). (b) Meanwhile, Toon, Robock & Turco do not factor in the possibility of counterforce targeting at all; conversely, it is the only one to take into account the projected future Chinese arsenal after growth through the 2020s. (c) Finally, the JCS estimate is extremely out of date, and does not consider changes in US nuclear posture, even while relying on fairly uncertain extrapolations. Given these flaws, I ultimately end up penalizing the Kristensen, Norris & McKinzie estimate once, and the JCS estimate twice over, yielding an aggregate estimate of 206 million violent deaths from US-China nuclear war.
• India-Pakistan nuclear war: For direct violent deaths from India-Pakistan nuclear war, I once more look at three different estimates. (a) First, there is the Toon et al estimate, of 87.5 million deaths, calculated by averaging the upper and lower bound fatality estimates. (b) Second, there is the US intelligence estimate, of 10.5 million deaths, again calculated by averaging the upper and lower estimates. (c) Third, there is the McKinzie et al estimate, of 2.9 million deaths. In aggregating these different estimates, I note the following points. Both the US intelligence estimate as well as the McKinzie et al estimate are considerably out of date, with their calculations performed using far smaller India/Pakistan arsenals. Moreover, McKinzie's estimate of the number of warheads deployed is fairly arbitrary. Hence, relative to the Toon et al estimate, I penalize the US intelligence estimate once, and the McKinzie estimate twice over, yielding an aggregate estimate of 79.8 million violent deaths from India-Pakistan nuclear war.

After this, the individual outcomes (i.e. NATO/Russia nuclear war, US/China nuclear war, and India/Pakistan nuclear war) are each weighted by the relative probability of occurrence, yielding an overall estimate of 99.5 million total direct violent deaths from an average nuclear war.

For indirect famine deaths due to nuclear winter causing agricultural failure, I once more look at the same three potential nuclear conflicts of  NATO-Russia, US-China & India-Pakistan.

• NATO-Russia nuclear war: For indirect famine deaths from NATO-Russia nuclear war, I similarly look at three different estimates. (a) First, there is the Xia et al estimate, according to which nuclear war would cause starvation that would kill more than 5 billion people in the case of a US-Russia nuclear war. (b) Second, there is the Rodriguez estimate, of 5.5 billion deaths. (c) Third, there is the Harwell estimate (as adjusted for population growth since) of 1.65 billion deaths. In aggregating these different estimates, I note the following points. The Xia et al estimate potentially overstates the damage in a US-NATO war insofar as it factors in attacks on China as well, and is hence penalized when incorporated in the aggregate. Meanwhile, the Harwell estimate appears far less quantitatively rigorous, and is extremely penalized relative to the baseline. Overall, this yields an aggregate estimate of 5.45 billion dead from starvation from NATO-Russia nuclear war.
• US-China nuclear war: For indirect famine deaths from US-China nuclear war, there do not appear to be direct empirical estimates of the climactic fallout of any such war. In lieu of that, I perform an indirect estimate anchored on the NATO-Russia figures. Per Toon, Robock & Turco, historical surveys as well as the known quantity of flammable material stored in the world suggests that the amount of fuel per unit area in the urban developed world is a linear function of population density. At the same time, area in km2 hit by nuclear weapons will scale with the number of warheads deployed in war. Hence, by adjusting the NATO-Russia figures with relative urban population density (as weighed by urban population) and relative number of warheads deployed in war, we can estimate the nuclear winter fatalities from a US-China nuclear exchange – perhaps 5.48 billion dead from starvation after such a war.
• India-Pakistan nuclear war: For indirect famine deaths from India-Pakistan nuclear war, I return to taking three separate estimates. (a) First, there is the Xia et al estimate, according to which nuclear war would cause starvation that would kill more than 2 billion people in the case of an India-Pakistan nuclear war. (b) Second, there is the Robock & Toon estimate, of 1 billion dead. (c) Third, there is the Helfand estimate, also of 1 billion deaths. In aggregating, I note that Helfand's estimate appears less quantitatively rigorous, and it is penalized accordingly, yielding an estimate of 1.48 billion dead from starvation from India-Pakistan nuclear war.

After this, the individual outcomes (i.e. NATO/Russia nuclear war, US/China nuclear war, and India/Pakistan nuclear war) are again each weighted by the relative probability of occurrence, yielding an overall estimate of 3.12 billion total indirect famine deaths from an average nuclear war.

Summing up both the direct violent deaths as well as the indirect famine deaths, this gets us to 3.22 billion total deaths from the average nuclear war in the baseline year of 2024.

Persistence: Naturally, the risk of nuclear war persists from year to year, and correspondingly the benefit of eliminating such risk would counterfactually stretch over time as well. In terms of how this multi-year benefit is calculated:

Firstly, I discount for the probability of the solution not persisting – specifically, for the likelihood of weapon stockpiles being expanded again even after initial arms limitation success via treaty (n.b. the choice of this particular solution will be discussed and justified at greater length subsequently). To calculate this discount rate, I look at the rate at which nuclear arms control treaties agreed to and put into effect by the US & Russia have been abrogated, by taking the years in which abrogation occurred and divided by the total number of years in which abrogation could have occurred but didn't. This reversal rate discount, so to speak, comes out to about 2% per annum.

Secondly, I discount for the proportion of problem being counterfactually solved. There are three aspects to this.

• Nuclear weapons stockpile growth: The problem might counterfactually be getting better nuclear weapon stockpiles diminishing even absent intervention (or conversely, getting worse if stockpiles are growing). I take an aggregated approach to this problem, by looking at the historical trend in the growth and decline of nuclear weapons. Theoretically, any efforts by various agents to reduce or increase nuclear weapon stockpiles (e.g. governments acting on reduction or expansion depending on perceptions of national interest, or nonprofits successfully lobbying for arms control, or defence contractors that produce nuclear-adjacent weapon systems pushing for expansion or at least maintenance of existing stockpiles) as well as any effects by long-term structural trends (e.g. economic growth increasing the chance of democratization and hence democratic peace, thus reducing security concerns and increasing the odds of denuclearization; and also cultural shifts bringing increased liberalization and hence political leaders' willingness to denuclearize) will put upwards/downwards pressure on the observable trend of past nuclear weapons stockpile growth. By projecting this trend into the future, therefore, we would implicitly be taking into account all these various agentic and structural factors going forward. As it happens, taking panel data of countries' nuclear weapon stockpiles from 1945-2022 and running a linear regression of stockpiles on year, we see that there is no sign of a statistically significant decline or increase (p=0.88). Hence, this discount factor here is assigned a 0 (i.e. we assume that nuclear weapon stockpiles aren't systematically growing or declining globally, even if individual countries may see drastic increases or cuts).
• Population growth: Here, we have to consider the proportion of population relative to the 2024 base, as more people alive means more people who can be harmed by nuclear war (or conversely, benefited by nuclear weapons averting conventional war). The analysis here pulls from UNPD estimates of projected future population growth up to 2100 and then thereafter takes that there is convergence to total fertility rate of 1.5 (given current high-income country fertility rates) and hence a -0.76% per annum decrease in population after 2100. Refer to Diagram 1 below for an illustration of global population growth from 2024-2100.

Diagram 1: Global population growth, 2024-2100

• Median age: Demographically, we must also consider the ageing of the global population relative to the 2024 base, as a higher median age means the average person saved will have fewer healthy years of life to live. The analysis here pulls from UNPD estimates of median age up to 2100 and then assumes constancy thereafter due to lack of reliable estimates. Overall, a discount rate of 0.4% per annum is used.

Thirdly, I discount for the probability of the world being destroyed anyway (i.e. general existential risk discount). This takes into account the probability of total nuclear annihilation, since the benefits of saving people from nuclear war in one year is nullified if they had already died in a previous year. For the exact risk of total nuclear annihilation, I take it to be one magnitude lower than the risk of nuclear war itself (the calculations of which we discussed later), since nuclear war may not kill everyone. Of course, this probability will shift as a result of any efforts to denuclearize, but the chances of success are sufficiently small (as will be discussed) that it does not change materially change our results. Here, I do not take into account other existential risks like supervolcano eruption and asteroid impact, since the chances of those occurring at all is very marginal per Denkenberger & Pearce, let alone the chances of such events killing everyone and not just most people. AI risk is not included in this analysis as it is unclear as to the degree to which transformative AI (for which we have precise forecasts) translates to substantial existential risk (less precise forecasts). Overall, therefore, for simplicity, I treat the general existential risk discount to be just the risk of nuclear war but adjusted a magnitude down – 0.06% per annum.

Fourthly, I apply a broad uncertainty discount of 0.1% per annum to take into account the fact that there is a non-zero chance that in the future, the benefits or costs do not persist for factors we do not and cannot identify in the present (e.g. actors directing resources to solve the problem when none are currently doing so).

Then, by taking expected population growth in each year from 2024-2100, and applying the per annum discounts (i.e. solution reversal, nuclear stockpile growth, median age, existential risk & uncertainty), we can find the extent of the potential problem (relative to the baseline year) available for denuclearization to solve in each year.

Finally, by (a) summing these discounted per annum relative values for 2024-2100, and then (b) using a perpetual value formula for 2101 to infinity while taking into account post-2100 population decline, we see that the benefit of averting nuclear war fatalities will last for the equivalent of 52 baseline years.

Value of Outcome: Overall, the raw value of averting nuclear war fatalities is 4.88 * 10¹² DALYs.

Probability of Occurrence: Of course, nuclear war has only a slight chance of occurring per annum. To calculate this probability, I consult the outside view, the inside view, as well as various experts' perspectives.

• Outside view, historical use in war. The probability of nuclear weapons being used during war, as based on historical frequency, is 1.4%;
• Inside view: For nuclear war to occur, four critical steps must happen between two enemy nations: (i) initial conventional conflict; (ii) choice to escalate to tactical nuclear weapons (e.g. to achieve security objectives after loss at the conventional level); (iii) choice to escalate to strategic nuclear weapons (e.g. to punish enemy tactical nuclear use); and (iv) choice to escalate to full blown nuclear war (e.g. to punish enemy strategic nuclear weapon use). For (i), given 1.81 interstate conflicts per annum from 1946 to the present, and 193 countries (and hence 37,056‬ potential 1-on-1 wars per annum), then each country has about a 0.005% chance per annum of engaging in conventional conflict. Then, for steps (ii)-(iv), there is always a real but still fairly low chance that escalation occurs (e.g. you want to gain a conventional advantage via tactical nuclear use, but the risks of escalation are massive; you want to punish enemy tactical nuclear use via strategic nuclear use, but the risks of escalation are again massive; and you want to punish enemy nuclear attacks against one of your cities, but full blown nuclear war is obviously a global death sentence), such that ~10% would be reasonable for each step. This translates to around a ‭0.000005‬% chance per annum of full nuclear war per conflict dyad between nuclear powers. If we think of the number of total number of potential conflict dyads (i.e. NATO-Russia, US-China, US-NK, Russia-China, China-India, India-Pakistan), this sums to around a ‭0.00003‬% chance of nuclear war per annum.
• Expert survey, Lugar: The probability of nuclear attack, as based on expert survey (Lugar 2005), is 2.21%.
• Expert survey, Sandberg & Bostrom: The probability of nuclear war killing at least 1 million, as based on expert survey (Sandberg & Bostrom 2008), is 0.39%;
• Superforecaster prediction, Good Judgement Project: The probability of nuclear detonation by a state actor causing at least 1 fatality, as based on superforecaster predictions from the Good Judgement Project, is 0.4%

In aggregating the outside view, inside view, and other different perspectives, I note that each estimate has their strengths and weaknesses.

• The historical frequency estimate has some empirical grounding (vs inside views which are subject to inferential uncertainty), but is nonetheless biased upwards due to historical use being in a MAD-free context, even while not being an estimate of the probability of full scale nuclear war (as opposed to single strategic use, which would still need to escalate to full-blown levels) (overall, -1 magnitude penalty relative to baseline).
• I have less confidence in my inside view, relative to experts and superforecasters (-1 magnitude penalty relative to baseline).
• The Lugar expert estimate is also not an estimate of the probability of full scale nuclear war (as opposed to mere tactical use, which would still need to escalate to the strategic and full-blown levels) (-2 magnitude relative to baseline).
• The Sandberg & Bostrom expert estimate is similarly not an estimate of the probability of full scale nuclear war (as opposed to mere strategic use, which would still need to escalate to the full-blown levels) (-1 magnitude penalty).
• The superforecaster estimate too is not an estimate of the probability of full scale nuclear war (once more, as opposed to mere tactical use, which would still need to escalate to the strategic and full-blown levels) (-2 magnitude penalty). Note that with respect to forecaster accuracy vs expert accuracy, there does not seem to be a difference, with the best study finding that forecasters and health professionals performed similarly, while in other studies, experts had goals besides accuracy, or experts were too few to produce a good aggregate prediction. Hence, all else equal I have weighed forecaster and expert predictions with respect to the probability of nuclear war equally.

And with all things above considered, I end up giving greater weight to the historical perspective, the Sandberg & Bostrom expert estimate as well as my own more conservative estimate when aggregating, yielding a 0.6% probability of nuclear war per annum.

Expected Value: Hence, the expected value of averting nuclear war fatalities is 3.13 * 10¹⁰ DALYs.

Expected Benefit: Averting Nuclear War Injuries

The second benefit of eliminating the risk of nuclear war would be averting the nuclear war injuries that would otherwise occur. Overall, around 2.01 * 10⁸ DALYs are at stake here, with this benefit modelled as follows.

Moral Weights: I take the value of averting a typical injury for the rest of one person's life to be 6 DALYs. This is calculated as a function of (a) the average disability weight for all injuries; (b) a minor age-based philosophical discount; (c) assuming we save someone of the median age; and (d) assuming the median age is at the halfway mark to average age of death and that DALYs are equally distributed across age groups such that any additional injury or disease has the same proportional effect. For more details, refer to CEARCH's evaluative framework.

Scale: To calculate the scale of the problem, I look to calculate the injury-to-fatality ratio in nuclear war, and to apply it to the already-calculated fatalities figures. To obtain this injury-to-fatality ratio, I look at three separate estimates: (a) Wellerstein et al estimate's, for the case of NATO-Russia nuclear war; (b) Toon, Robock & Turco's estimate, for the case of US-China nuclear war; and (c) Toon et al's estimate, for the case of India-Pakistan nuclear war (averaging the injury-to-fatality ratios for both smaller and larger nuclear weapon explosions). In aggregating, I use equal weightage, yielding an average injury-to-fatality ratio in nuclear war of 1.02.

This lets us calculate the total injuries from an average nuclear war in the baseline year of 2024 – 101 million injuries – as it is a function of the average injury-to-fatality ratio in nuclear war as well as the average total direct violent deaths from nuclear war. 

Persistence: The same per annum discounts and projections of population growth, as discussed in the previous section on nuclear war fatalities, are used here as well, such that the benefit of averting nuclear war injuries will similarly last for the equivalent of 52 baseline years.

Value of Outcome: Overall, the raw value of averting nuclear war injuries is 3.14 * 10¹⁰ DALYs.

Probability of Occurrence: The probability of nuclear war is as calculated previously – 0.6% per annum.

Expected Value: All in all, the expected value of averting nuclear war injuries is 2.01 * 10⁸ DALYs.

Expected Benefit: Increased Economic Output

Beyond the health benefits, there are also economic benefits to eliminating the risk of nuclear war, as fewer deaths and injuries translate to more hours worked and higher productivity per hour. Around 7.35 * 10⁹ DALYs are at stake here, with the calculations as follows.

Moral Weights: I take the value of doubling consumption for one person for one year to be 0.21 DALYs. This is calculated as a function of (a) the value of consumption relative to life from GiveWell's IDinsight survey of the community perspective, as adjusted for social desirability bias, and (b) CEARCH's estimate of the value of a full, healthy life in DALY terms. For more details, refer to CEARCH's evaluative framework.

Scale: The approach I take is to estimate the average degree of consumption doubling per DALY lost, and to apply it to the already calculated DALYs lost to nuclear war on both the mortality and morbidity fronts. To estimate this, I look at three different reference classes from global health – hypertension, diabetes mellitus type 2, and coronary heart disease – which yields an average of 1.11 consumption doublings per DALY lost.

This lets us estimate the total number of consumption doublings achievable by eliminating the risk of nuclear war in the baseline year of 2024 – 106 billion – calculated as the degree of consumption doubling per DALY and the total number of DALYs lost both to mortality (fatalities) and morbidity (injuries).

Persistence: The same per annum discounts and projections of population growth, as discussed in the previous section on nuclear war fatalities, are used here as well, such that the benefit of averting nuclear war injuries will similarly last for the equivalent of 52 baseline years.

Value of Outcome: Overall, the raw value of averting nuclear war injuries is 1.15 * 10¹² DALYs.

Probability of Occurrence: The probability of nuclear war is as calculated previously – 0.6% per annum.

Expected Value: All in all, the expected value of averting nuclear war injuries is 7.35 * 10⁹ DALYs.

Expected Cost: More Conventional War Fatalities

We've been discussing the benefits of denuclearization, but it is important not to forget that it does come with a downside, insofar as nuclear weapons help deter conventional conflict between the nuclear powers. Consequently, the first and primary expected cost of eliminating the risk of nuclear war is more conventional war fatalities. Overall, around -1.43 * 10⁵ DALYs are at stake here, with this cost modelled in the following way.

Moral Weights: The disvalue of one death is -29.3 DALYs, as calculated in the manner described in the section on nuclear war fatalities.

Scale: For the scale of the cost, I examine the average deaths per conventional war; in particular, I look at the Conflict Catalogue for the past 100 years (1923-2022) for conflicts where data is available, and find that the average conflict cost around 311,000 lives.

Persistence: The same per annum discounts and projections of population growth, as discussed in the previous section on nuclear war fatalities, are used here as well – except in the case of counterfactual solution, where we have to look at conventional war becoming less likely.

I take an aggregated approach to this problem, by looking at the historical trend in the growth and decline of conventional warfare. Theoretically, any efforts by various agents to make more war less likely (e.g. regular diplomatic efforts by governments, or lobbying by anti-war non-profits and also by businesses wary of the cost of war), as well as any effects by long-term structural trends (e.g. economic growth increasing the chance of democratization and hence democratic peace, thus reducing security concerns and decreasing the odds of conventional war; and also cultural shifts bringing increased liberalization and hence political leaders' unwillingness to go to war) will put upwards/downwards pressure on the observable trend of deaths and injuries (and hence DALYs) lost per capita to conflict. By projecting this trend into the future, therefore, we would implicitly be taking into account all these various agentic and structural factors going forward. As it happens, by regressing 1990-2019 GBD data on conflict and terrorism on year, we find no statistically significant trend (p=0.2). Hence, this discount factor here is assigned a 0 (i.e. we assume that conventional warfare is not getting better or worse per capita).

Overall, therefore, the cost of more conventional war fatalities will end up lasting for the equivalent of 52 baseline years.

Value of Outcome: Overall, the raw value of more conventional war fatalities is -4.71 * 10⁸ DALYs.

Probability of Occurrence: To estimate the reduced probability of conventional conflict as a result of nuclear weapons, I rely on Sobek, Foster and Robison's analysis, with my approach as follows. (a) I treat the control risk to be the "explore" phase, on the basis that countries would choose to explore the acquisition of nuclear weapons because there is a legitimate security threat that the country would have to worry about anyway even if they did not pursue nuclear weapons. (b) I compare this to the risk of war after acquisition. (c) Then, I take the difference to be the reduced probability of conventional conflict as a result of nuclear weapons. The results are multiplied by 6 given the relevant dyads of nuclear powers that would otherwise potentially go to war against each other (i.e. NATO-Russia, US-China, US-NK, Russia-China, China-India, India-Pakistan). The effect of nuclear weapons on conflict between nuclear and non-nuclear powers is not modelled here, insofar as theoretically it is both plausible that nuclear weapon states feel emboldened to start conflicts against non-nuclear states even as non-nuclear states are more averse to fighting their nuclear-armed foes, leaving the effect ambiguous. Overall, the reduced probability of conventional war per annum is 0.03%.

Expected Value: All in all, the expected value of more conventional war fatalities is -1.41 * 10⁵ DALYs.

Expected Cost: More Conventional War Injuries

The second expected cost of eliminating the risk of nuclear war is more conventional war injuries. Overall, around -6.89 * 10⁴ DALYs are at stake here, with this cost modelled as follows.

Moral Weights: The disvalue of a typical injury for the rest of one person's life is -6 DALYs, as calculated in the manner described in the section on nuclear war injuries.

Scale: For the scale of the cost, I estimate the injury-to-fatality ratio in conventional war, by using Khorram-Manesh's systematic review of the ratio of deaths to total casualty in major terror attacks, which is around 2.38.

This allows us to then calculate the average number of injuries per conventional war – around 739,000 injuries – as it is a function of the injury-to-fatality ratio in conventional war and the average deaths per conventional war.

Persistence: The same per annum discounts and projections of population growth, as discussed in the previous section on conventional war fatalities, are used here as well, such that the benefit of averting conventional war injuries will similarly last for the equivalent of 52 baseline years.

Value of Outcome: Overall, the raw value of more conventional war injuries is -2.3 * 10⁸ DALYs.

Probability of Occurrence: The reduced probability of conventional war due to nuclear weapons is as calculated previously – 0.03% per annum.

Expected Value: All in all, the expected value of more conventional war injuries is -6.89 * 10⁴ DALYs.

Expected Cost: Decreased Economic Output

The third expected cost of eliminating the risk of nuclear war is decreased economic output, since parallel to the nuclear case, more deaths and injuries translate to fewer hours worked and lower productivity per hour. Overall, around -4.91 * 10⁴ DALYs are at stake here, with the calculations as follows.

Moral Weights: The disvalue of not doubling consumption for one person for one year is -0.21 DALYs, as calculated in the manner described in the section on increased economic output due to less mortality and morbidity from nuclear war.

Scale: The total number of consumption doublings lost from more conventional war in the baseline year of 2024 is 15.1 million; this is calculated as the degree of consumption doubling per DALY and the total number of DALYs lost both to mortality (fatalities) and morbidity (injuries).

Persistence: The same per annum discounts and projections of population growth, as discussed in the previous section on conventional war fatalities, are used here as well, such that the benefit of decreased economic output will similarly last for the equivalent of 52 baseline years.

Value of Outcome: Overall, the raw value of decreased economic output is -1.64 * 10⁸ DALYs.

Probability of Occurrence: The reduced probability of conventional war due to nuclear weapons is as calculated previously – 0.03% per annum.

Expected Value: All in all, the expected value of more conventional war injuries is -4.91 * 10⁴ DALYs.

Tractability

To summarize our tractability findings: we can solve 0.007 of the problem with a USD 17.6 million investment into advocacy for nuclear arsenal limitation, which means the proportion of the problem solved per additional USD 100,000 spent is around 0.00009.

At the outset, we should note that there are a number of potential interventions to reduce the risk of nuclear wer: (a) abolishment (i.e. eliminating all nuclear weapons); (b) limitation (i.e. limiting but not eliminating nuclear weapon arsenals); (c) targeting reform (i.e. getting countries to shift to potentially less damaging counterforce rather than countervalue targeting); and (d) mitigation (i.e. looking to deal with the famine caused by nuclear winter rather than trying to prevent it in the first place).

• For (a), as Rodriguez notes, it is unlikely that countries that are non-compliant with the Treaty on the Prohibition of Nuclear Weapons will ratify it, or that TPNW supporters will be influenced not to pursue, host or manufacture nuclear weapons or to join a nuclear weapons alliance. In short, existing nuclear abolishment efforts are ineffective, suggesting that progress is fundamentally intractable. Quantitatively, per CEARCH's previous analysis, abolishment's marginal expected value is 248 DALYs per USD 100,000 spent, making it only 40% as cost-effective as a GiveWell top charity (i.e. not worth supporting).

• To choose amongst (b)-(d) then, and to select the potential best solution which we can then prioritize for actual evaluation, we can look at (i) degree of risk reduction, and (ii) cost.
  
  On (i) risk reduction (note: here, we focus on the primary harm of deaths from famine rather than from direct nuclear fire, while also factoring out probability of advocacy success insofar as all solutions appear similarly difficult): Let us say that the Chinese arsenal (~350 warheads) is sufficient for deterrence (n.b. my considered view is that direct US nuclear attack on China would be unthinkable given the risk of Chinese nuclear retaliation with this arsenal, and that even conventional attacks on the mainland would be extremely unlikely except in the case of the outbreak of hostility e.g. from a pre-emptive Chinese attack on American forces as the prelude to an invasion of Taiwan, but especially from a successful sinking on a US carrier). One potential avenue for risk reduction, then, is nuclear arms limitation by the US and Russia to current Chinese levels, and a commitment by the Chinese not to expand their arsenal beyond that.
  
  In terms of the effect of such a limitation, to the extent that a first strike by the US on Russia or vice versa will involve around 1200 warheads each, and assuming that smoke produced is proportional to number of detonations, we are looking at a potential 71% reduction in risk. Meanwhile, with respect to the impact of countervalue vs counterforce targeting, Russia engages in countervalue targeting while the US is counterforce. Based on the amounts of smoke that would be produced under full counterforce vs full countervalue targeting, this translates to a reduction from the status quo of 19.9 tg of smoke produced in US-Russia nuclear war to a reduced risk scenario of 8.8 tg of smoke - a 56% reduction in risk. Finally, for mitigation, using resilient foods in the manner described by ALLFED would be able to meet the global caloric requirements and hence avoid any starvation at all - and hence a potential 100% reduction in risk.
  
  Now, moving on to (ii) cost - this is hard to quantify, but my sense is that (d) will be magnitudes more expensive than (b) or (c), involving as it does large scale changes to the global food supply system, even as the other two involve merely changes in force postures (trivial costs) as in the case of (c), or else no net costs (with disposal & monitoring costs offset by no longer having to pay for maintenance and modernization at the very least) as in the case of (b). Since (d) is only 1.41x and 1.79x more impactful than (b) and (c) respectively, even while (d) is likely magnitudes more expensive, the question reduces to (b) vs (c), and (b) is of course more impactful with 71% risk reduction vs 56%.
  
  Hence, solution (b) of limitation in nuclear arms - specifically, getting the US/Russia/China to adhere to a 350 limit - is chosen as the potential best solution to be evaluated in depth here.

In terms of our theory of change:

• Step 1: Persuade the United States, Russia and China to limit the size of their nuclear arsenals.
• Step 2: The United States, Russia and China limiting the size of their nuclear arsenals reduces the expected harm of nuclear war.

Note that whether commitments by the US/Russia/China translate to actual limitations is not modelled here, as it is already taken into consideration by the incorporation of a reversal rate in the analysis of the various expected benefits (i.e. averting nuclear war fatalities and injuries, or increased economic output) – to the extent that the US/Russia/China renege on their promises, it will cause counterparty withdrawal, a breakdown of the agreement, and an end to the benefits, as modelled.

Step 1: To estimate the probability of persuading the United States, Russia and China to limit the size of their nuclear arsenals to present Chinese levels, I take both the outside and inside view.

For the outside view, I consult three reference classes.

• Nuclear arms control: The ability of nuclear doves within the US/Russia governments to convince hawks on the other side (as well as get buy in from hawks on their side) is a relevant indicator of the ability of outside parties to do the same and hence successfully obtain nuclear arms limitations. To quantify this, I look at the years in which nuclear control treaties were signed, and divide through by the years in which said treaties were negotiated (whether successfully or not).
• Chemical weapons control: The success of WMD control advocates in the area of chemical weapons is also relevant, and here I look in particular at the process which brought the Chemical Weapons Convention into force, with negotiations beginning in 1981 and the US/Russia signing in 1993. I take the success rate to be the year in which signing occurred by the US/Russia, divided by the years in which they could have signed whether they actually did or not.
• Biological weapons control: The success of WMD control advocates in the area of biological weapons is also relevant, and here I look in particular at the process which brought the Biological Weapons Convention into force, with negotiations beginning in 1969 and the US/Russia signing in 1972. I take the success rate to be the year in which signing occurred by the US/Russia, divided by the years in which they could have signed whether they actually did or not.

In aggregating, a higher weight is placed on the actual nuclear case study compared to the chemical and biological ones, as security considerations militate against denuclearization in a way they do not for chemical and biological weapons, making the weapons control efforts for the latter two areas unrepresentative of success on the nuclear front. This yields a probability of advocacy success of 17%.

For the inside view, I break this problem down into three separate steps: (a) persuading the US to reduce the size of its nuclear arsenal conditional on Russia and China agreeing to limits as well; (b) persuading Russia to reduce the size of its nuclear arsenal conditional on the US and China agreeing to limits as well; and (c) persuading China not to continue nuclear expansion from its present arsenal size conditional on the US and Russia agreeing to limits as well.

• In each case, at the outset it is important to note that policy advocacy is hard, and will be at <=10% chance of success.
• More than that, however, nuclear weapons make strategic sense from each great power's point of view. In general, nuclear weapons are of increasing strategic value to ambitious autocrats hoping to pursue opportunistic aggression and risk manipulation - Putin and Xi or their successors see nuclear weapons as critical tools when it comes to asserting control over the post-Soviet states or to ensuring Taiwanese reunification, and on the flipside, because of the risk of non-conventional revanchist aggression, the United States will value its own nuclear weapons as a shield for its allies in Europe (e.g. Poland and the Baltics) and in East Asia (e.g. Japan, who will be attacked in the event of a Chinese attempt on Taiwan); and with the greatest nuclear weapon powers valuing nuclear weapons as useful tools to safeguard national interests, they will see little reason to reduce the size of their arsenals, and are hence unlikely to agree to nuclear arms limitations. Hence, I calibrate the rate of advocacy success further to 1%.
• But further, country-specific factors make things even more pessimistic. For the US, Eastern European allies might perceive any overtures to Moscow for dialogue as concessionary or a sign of waning U.S. commitment; for Russia, following the war in Ukraine, Russia’s conventional forces will likely be depleted, and it may react by increasing reliance on its nuclear deterrent; and for China, the transparency that typically accompanies arms control goes against current Chinese practices. Accordingly, I adjust the rate of advocacy success to 0.1% for Russia, 0.3% for China, and 0.7% for the US.

Multiplying these rates together yields the probability of persuading the United States, Russia and China to limit the size of their nuclear arsenals: 0.0000021%

In adjusting the outside view with the inside view, we must note that the inside view is subject to the usual worries about inferential uncertainty. However, the outside view in this case is also flawed. Firstly, selection bias is a serious concern, insofar as the nuclear arms control treaties that were successfully negotiated would only have been tried in the first place because political sentiment was favourable/permissible, and it would be very different to an arms control effort being tried in a vacuum. Secondly, these are all examples of government-initiated efforts, which skips the crucial step of outside actors persuading governments to try in the first place. Consequently, I end up weighing the far more conservative inside view more than the comparatively optimistic outside view – yielding a probability of advocacy success of 1.5%.

Step 2: For the degree to which the United States, Russia and China limiting the size of their nuclear arsenals reduces the expected harm of nuclear war, I rely on an empirical estimate. The primary modelled scenario in NATO-Russia nuclear war is Russia targeting 1000 weapons on the US while the US retaliates with 1100 weapons on Russia; and as for US-China nuclear war, the scenario considered is a 1100 warheads US attack on China and 1000 warhead Chinese attack on the US, given the projected Chinese arsenal by 2030. With all parties limited to 350 weapons, the expected harm from nuclear war falls (though correspondingly, the expected cost from less deterrence potentially falls as well, since the costs of conventional aggression, which risks nuclear war, are correspondingly less daunting), assuming harm is linear with the number of weapons. Then, by taking into account the relative proportion of the problem caused by potential NATO-Russia and US-China nuclear war rather than India-Pakistan nuclear war, the overall proportion of the problem being solved can be calculated at around 48%.

Overall, the proportion of nuclear war harm solved – as a function of (a) the probability of persuading the United States, Russia and China to limit the size of their nuclear arsenals; and (b) the degree to which the United States, Russia and China limiting the size of their nuclear arsenals reduces the expected harm of nuclear war – is 0.007.

Turning to the issue of costing, I look at two reference classes to estimate the money required to conduct lobbying (i.e. how much it would cost to run an EA advocacy organization working on the issue):

• Reference class of existing charity: I look at ICAN, which appears the top charity working in this area. Taking its 2021 net expenses in francs, converting to USD, and taking 10 years for success (on the basis that that was how long it took ICAN to pass the TPNW, with its founding in 2007 and the TNPW passed in 2017), that yields the relevant total cost of around USD 20.1 million.
• Reference class of hypothetical CE-incubated charity: My sense is that you would want a team of maybe 10 people working in each country, and that they would need perhaps 10 years or so to succeed. Each team member is estimated to cost around USD 50,000 per team member per annum, in line with past CE incubatee expenditures, which yields a total cost of USD 15 million.

In aggregating, we have to consider that (a) on the one hand, the existing organization's financial track record generally gives a much better indication of baseline expenditure requirements in the cause area; and (b) on the other hand, the explicitly EA-aligned CE-incubatee will almost certainly be more cost-effective. Hence, I ultimately use equal weightage, which yields a total cost of USD 17.6 million. Note that we do not look at implementation costs because as mentioned above, actually nuclear arms reductions saves money.

Consequently, the proportion of the problem solved per additional USD 100,000 spent is around 0.00009.

Marginal Expected Value of Lobbying for Arsenal Limitation to Mitigate Nuclear War

All in all, the marginal expected value of lobbying for arsenal limitation to mitigate nuclear war is 3,341,695 DALYs per USD 100,000 spent, making this around 5000x as cost-effective as a GiveWell top charity.

Vasco Grilo @ 2023-03-31T19:09 (+2)

Nice analysis, Joel!

For indirect famine deaths due to nuclear winter causing agricultural failure

FWIW, I have also estimated the deaths due to a nuclear winter here:

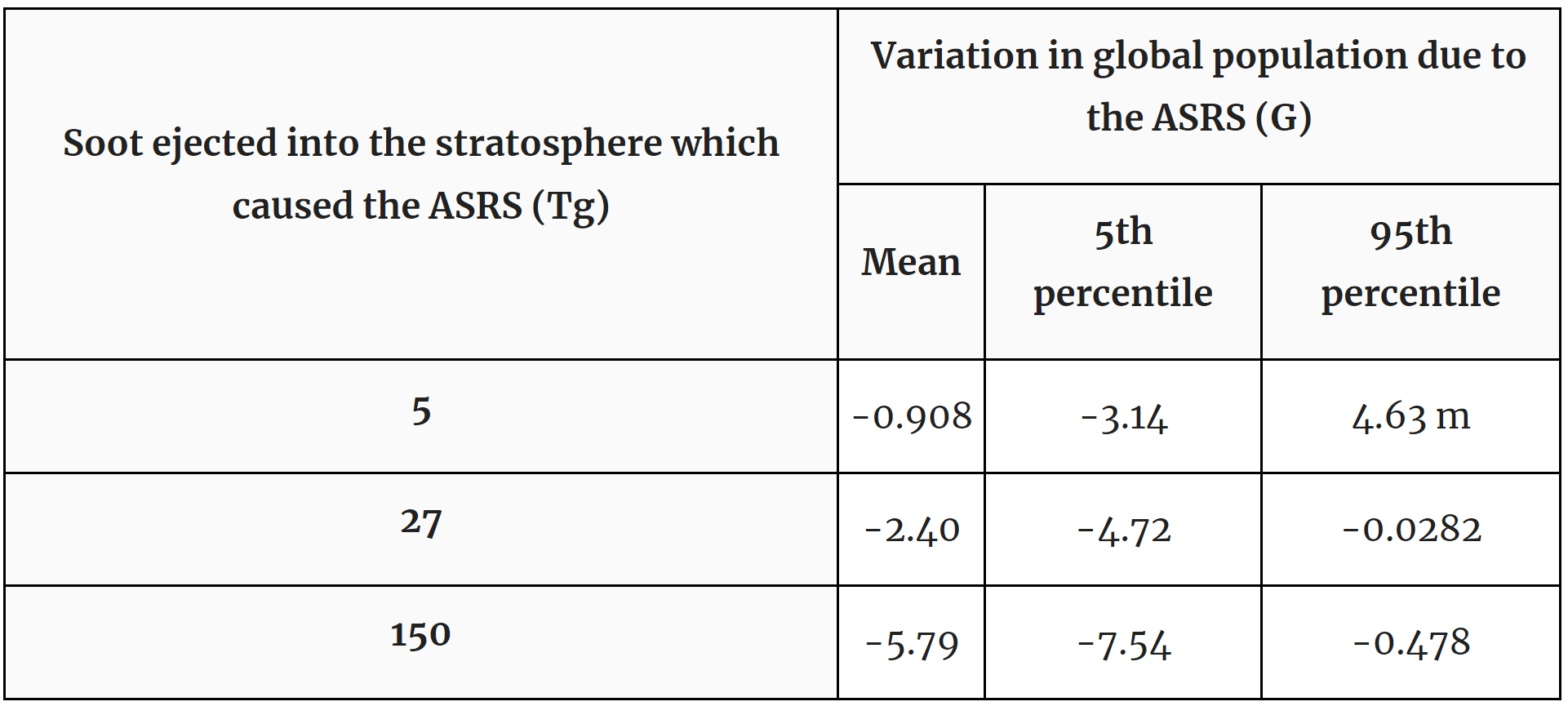
So, for Luisa's mean soot ejection of 30 Tg for a NATO-Russia nuclear war (search for "30 Tg of smoke (" here), I get roughly 2.4 billion deaths.

As it happens, taking panel data of countries' nuclear weapon stockpiles from 1945-2022 and running a linear regression of stockpiles on year, we see that there is no sign of a statistically significant decline or increase (p=0.88). Hence, this discount factor here is assigned a 0 (i.e. we assume that nuclear weapon stockpiles aren't systematically growing or declining globally, even if individual countries may see drastic increases or cuts).

I think a rule like the following is too binary:

• If p < 0.05, account for the effect.
• If p > 0.05, set the effect to zero.

I think it would be better to model the change in nuclear weapons based on future forecasts. Metaculus' pro forecasters predicted a median of 6.20 k for 2052, and 1.70 k for 2122 (search for "Global Nuclear Warhead Stockpiles" here). To model uncertainty (maybe we should indeed expect the number to be roughly constant), one could use the 25th and 75th percentile from Metaculus' forecasts. I did this here, and arrived at a mean number of nuclear warheads from 2024 to 2100 relative to 2019 of 84.4 %. This is pretty close to 1, so at the end I do not think this is a super important factor.

Probability of Occurrence: Of course, nuclear war has only a slight chance of occurring per annum. To calculate this probability, I consult the outside view, the inside view, as well as various experts' perspectives.

You may also want to consider this Metaculus' question, whose median community prediction yields a annual chance of 0.272 % (= 1 - (1 - 12 %)^(1/(2070 - 2023))), which is about half your final estimate.