Conditional Forecasting As Model Parameterization

By Molly Hickman @ 2025-04-18T02:32 (+10)

This is a linkpost to https://cuttyshark.substack.com/p/conditional-forecasting-as-model

This work was done jointly with Rajashree Agrawal. We'd like to thank the Epoch AI summer mentorship project, led with Forecasting Research Institute, for introducing us. Thanks to Josh Rosenberg, Tegan McCaslin, Avital Morris and others at FRI, as well as Jaime Sevilla at Epoch AI. Thanks also to Misha Yagudin and Jonathan Mann for their feedback.

This is the second piece in a series on forecasting, especially conditional forecasting and the potential we see there for making fuzzy models more legible:

1. Forecasting: the way I think about it
2. The promise of conditional forecasting for parameterizing our models of the world [this post]
3. What we're looking at and what we're paying attention to (Or: Why we shouldn't expect people to agree today (Or: There is no "true" probability))

TL;DR: Where the market can't converge on decent forecasts, like on very long-run questions or questions involving disruptive technology, we need better ways to wring forecasts and models out of informed people. In this post we present one approach that serves to surface and refine experts' implicit models.

This has been in my drafts for so long that there has been a lot of awesome work on this problem in the meantime, at Metaculus (my current employer), the RAND Forecasting Initiative, the Forecasting Research Institute, and elsewhere. I'm not going to talk about any of that work in this piece, in the interest of getting it out the door! I'm just focusing on the work Rajashree and I did between summer 2023 and summer 2024.

Introduction

In the first post, we talked about one way to come up with one single forecast: thinking about different worlds, what would happen in each world, and how likely each world is to manifest. In this post we're going to talk about how we see conditional forecasting as the key to a) eliciting expert's models better and b) comparing any two people's models to each other.

The foundational literature (e.g. Goldstein et al, Karvetski et al, Tetlock's Expert Political Judgment) in Tetlockian forecasting seems to point at the top forecasters having better understanding of how the world works than domain experts (if you're on board with the idea that proper scores, in this case Brier,^[1] are a reasonable proxy for "understanding of how the world works"). Despite lacking the years of knowledge, experience, and gut-feelings that experts have, forecasters are better at putting numbers to whatever knowledge, experience, and gut-feelings they do have—implying that high-quality expression of shallow information > low-quality expression of deep information. This makes some intuitive sense; for instance, despite farmers' having much deeper understanding of agriculture, it doesn't seem like they're better at crop futures trading than traders.

This presents an obvious opportunity to improve the discourse and better understand what to expect in the world and why: Help experts better express their models and elicit their latent knowledge, analogous to mech interp on human intuition.

Point forecasts, without much/any rationale, are cheap. It's expensive to get people to try to articulate the reasoning behind their forecasts. And point forecasts are often fine, especially when you're forecasting about a phenomenon that's basically well-understood (i.e. where the market can converge on decent things). But some phenomena are harder to predict using base rates or by reading the news; it's not obvious how to model them well. For high-stakes questions, we should be willing to invest in something slightly more involved.

This is especially relevant for disruptive technologies, where historical data provides limited guidance and expert intuition becomes crucial. Traditionally, we've divided forecasting problems into just two buckets: computable phenomena (like weather prediction) that yield to quantitative models, and non-computable phenomena (like geopolitical events) where we rely on expert judgment and crowd wisdom.

But reality is more nuanced. We can think of predictability as existing on a ladder. At the top rung are questions about phenomena where we have deep mechanistic understanding through science and mathematics, enabling widespread agreement on underlying processes. In the middle are phenomena like elections or economic indicators; while they resist quantitative modeling, we have enough collective experience that aggregating forecasts yields valuable insights. At the bottom rung are questions about emerging technologies and their complex societal effects—territory where experts disagree not just on probabilities but on fundamental causal mechanisms. We're interested in techniques for pushing things up the ladder—parameterizing people's fuzzy, qualitative models and revealing the mechanisms at play.

Expert Model Elicitation

One thing is certain: It's hard to get experts, or almost anyone, to articulate their beliefs as probabilities. Here's an idea, jumping off work the FRI has done vis-a-vis "value of information" (evaluating how good one forecasting question is, relative to another), that we think is really promising: probing for mutual information between questions as a way to find out what you think.

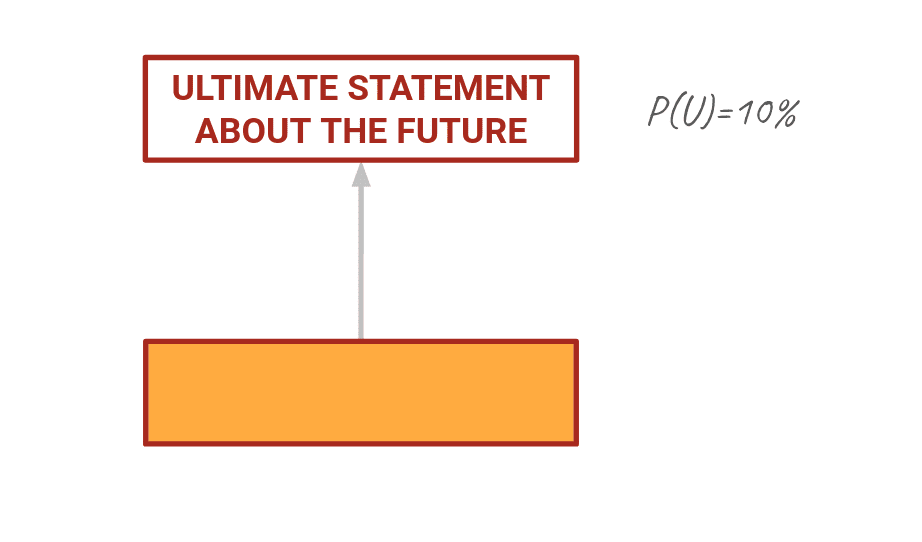
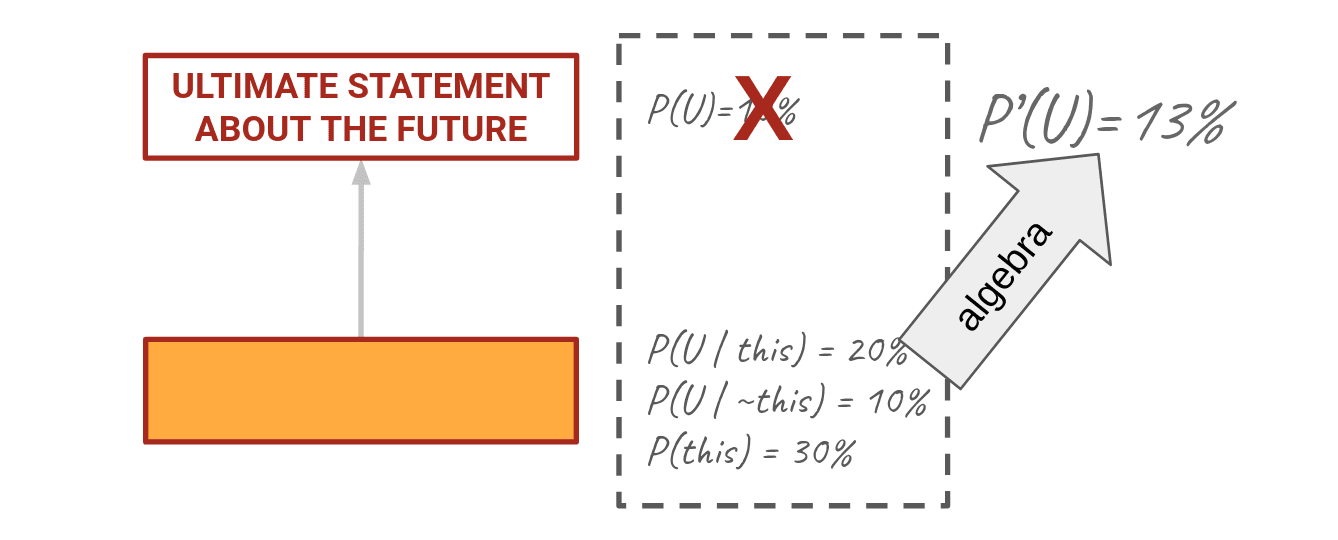
Let's say I'm an expert and I have information you want about an ultimate statement U. Initially I might say P(U) is like 10%, but I haven't thought about it very much yet. Orange box here, let's call him O, is something related to U that if I knew it was true would change my belief about U.

So I think about O—P(O)—and what I would think about U if I knew O was true—P(U|O)—and if I knew it was false—P(U|~O). Do a little algebra on that and you'll find a new P(U) of 13%. Thinking about O helped me clarify what I thought about U.

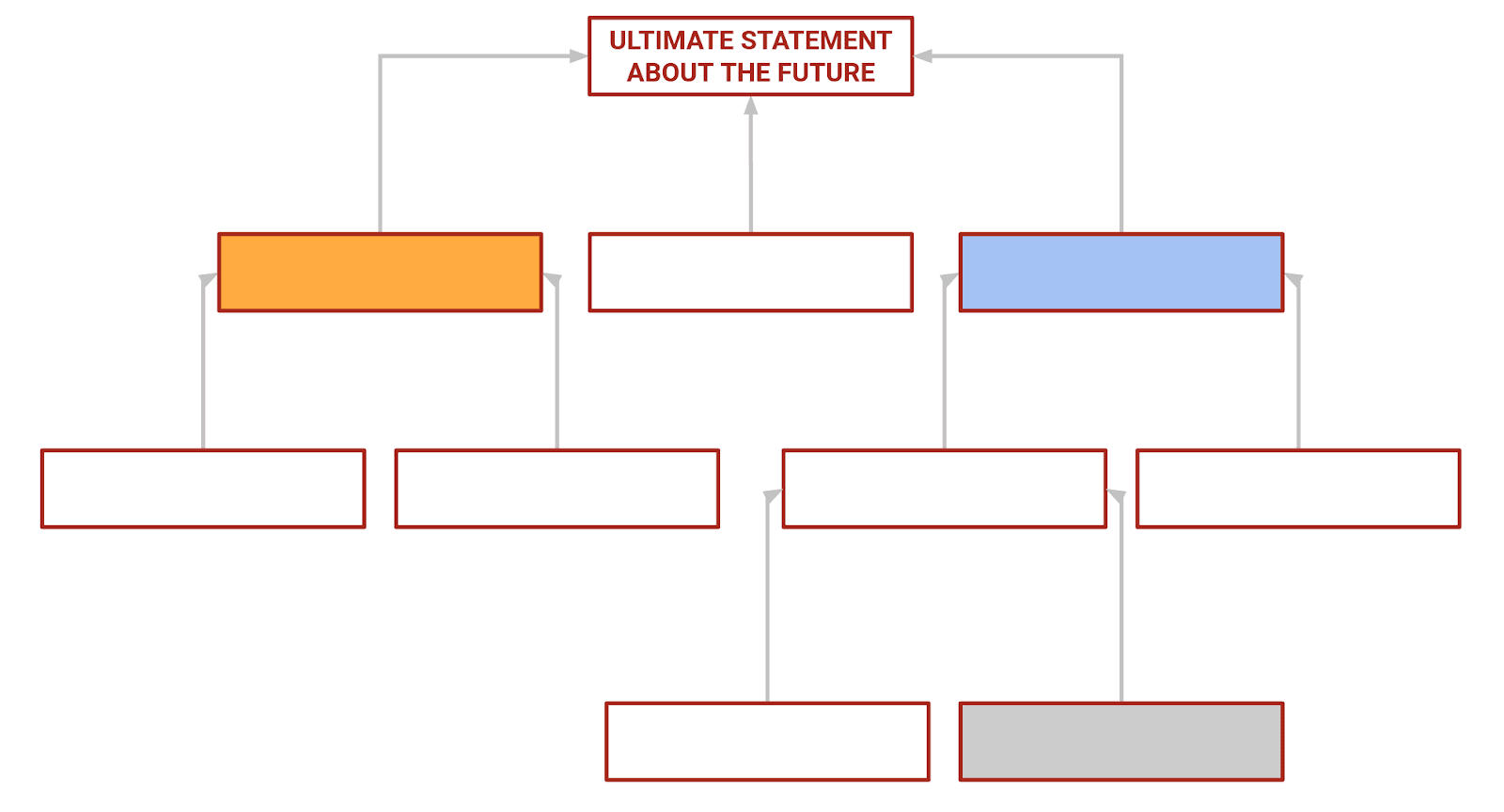
And we don't stop there! We can think about lots of things that would influence our feelings about U, and we can think more deeply about each of those things in turn, etc. Just keep adding levels to this graph, asking “why do I think this?” In the end we have a graph that looks something like this:

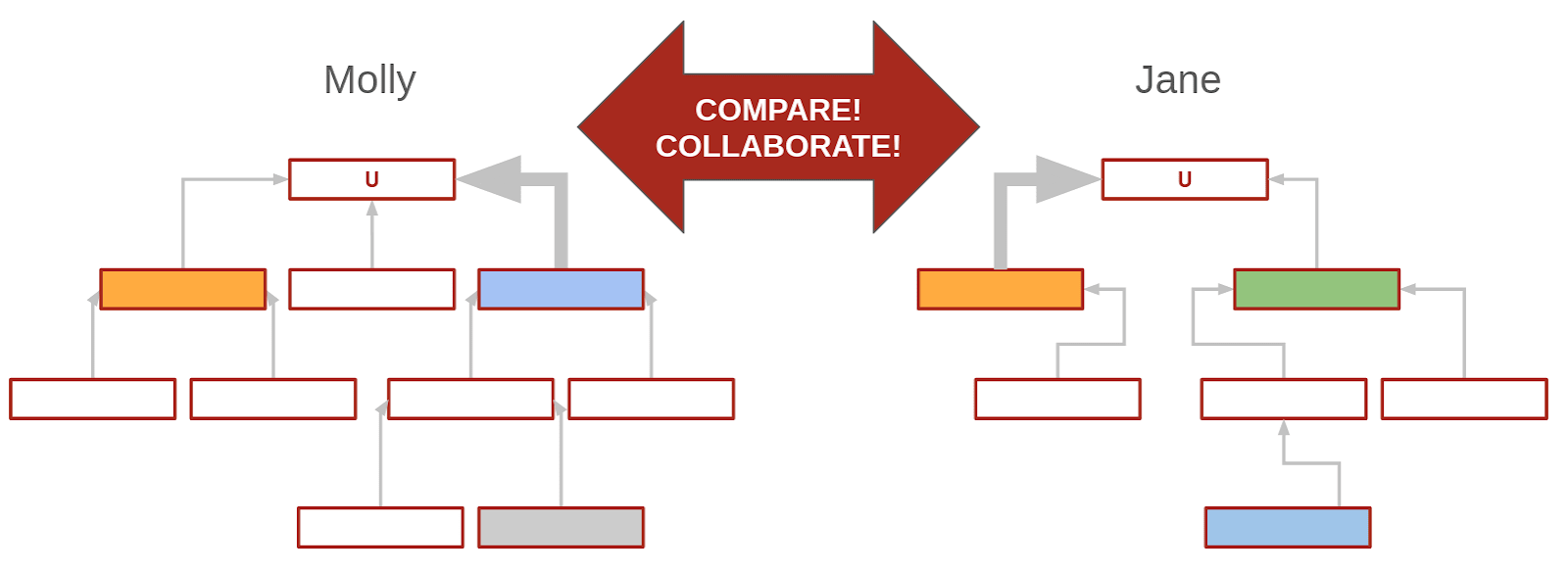
Now Julie and I can look at each other's models and zero in on our fundamental disagreements. For me, the blue crux represents the highest-VOI thing, or the relevant dominant uncertainty^[2]; for Jane it's the orange. I'm relatively uncertain whether it will happen or not, and whether it happens has a lot of bearing on my thoughts about U.

The green crux is part of Jane's model and not part of mine yet—it's something I haven't factored in yet. Maybe I want to add it to my model! Maybe I disagree with Jane about how likely it is to resolve positively or how it would affect U, but I should consider it. I could even try using the structure of Jane's model—we could call this her decomposition—and assigning my own probabilities to it; then see what I get.

Thinking with different primitives

As the age-old adage goes, "the best way to get the right answer on the internet is not to ask a question; it's to post the wrong answer."^[3] It's much easier to correct a flawed model than to generate our own.

One way that folks have tried to compare people's world models is to ask them a lot of conditional questions with the same consequent (or "parent" or "ultimate question"). Then we compare which antecedents are more important to whom. In a nutshell, this is what the Forecasting Research Institute did in their report Roots of Disagreement on AI Risk.

But you'll often find that when people disagree it's because they see the world differently—they think using different primitives. By "primitives," we mean the basic building blocks people use to construct their understanding of the world. These are the fundamental concepts, assumptions, and mental categories that form the foundation of how someone thinks about a topic.

Think of primitives as the core elements in someone's mental toolkit—like how a mathematician might use "sets" or "functions" as basic units to build complex theories, or how a physicist might think in terms of "forces" and "fields." When two people have different primitives, they're essentially using different mental languages to process the same reality.

The best questions are the ones that help you boil your model down into fewer parameters. To Arjun, two questions might be so correlated as to be redundant, while to Bernice they're both totally critical to how you see the world. This happens because Arjun's mental model might have a primitive concept that automatically links these questions (like "institutional competence" that applies to multiple scenarios), whereas Bernice might have separate primitives for each situation (like "government effectiveness in crisis A" and "government effectiveness in crisis B").

Instead of imposing the same "tree" on both of us, we could ask Arjun and Bernice to make forecasts on each other's trees and anchor their discussion there. Why do they disagree? Each question is a parameter. Is their disagreement about the parameters themselves? The weights on the parameters? The correlations between parameters? By exploring how each person organizes their thinking—what their basic primitives are—we can better understand where true disagreements lie rather than talking past each other

Nitty-gritty about how we measure "what's important"

This is math—you can skip this section if you don't care how we weight the edges of the graph.

First, let's define the terms:

• U - the ultimate question resolves "yes"
• A - a crux, antecedent, primitive, parameter, factor, consideration (it goes by many names)

For each of the antecedents, we’re taking the divergence between the product of the marginal distributions A and U (which assumes they’re independent events) and the joint distribution (which does not), so that we’re not eliciting any other causal information. If they're independent (i.e. A has no bearing on U, totally irrelevant), these two are the same; the more different they are, the more important A is to U. You have to ban As that have the same or overlapping measurement criteria as U (this might seem obvious but it's worth making explicit, e.g. you can’t have a crux be “U resolves positively and also this other thing happens”).

Importantly, this formula doesn’t enforce consistency. Instead, we treat inconsistent forecasts as information, i.e., if considering the antecedent changed your mind about the consequent, that indicates it's quite informative! You can find this and other formulations of Value of Information here (Forecasting Research Institute).

import math
def calculate_mutual_information(pu, pc, puc, punotc):
        """
        Calculate mutual information I(U;C) from P(U), P(C), P(U|C) and P(U|not C).
        Follows the implementation from forecastingresearch/voivod
        Parameters:
        -----------
        pu : float
            Probability of event U, P(U)
        pc : float
            Probability of event C, P(C)
        puc : float
            Conditional probability of U given C, P(U|C)
        punotc : float
            Conditional probability of U given not C, P(U|not C)
        Returns:
        --------
        float
            The mutual information I(U;C) in bits
        """
        # P(U|c)P(c) and P(U)P(c) terms
        puc_pc = puc * pc * math.log10((puc * pc) / (pu * pc))
        puc_pc += (1 - puc) * pc * math.log10(((1 - puc) * pc) / ((1 - pu) * pc))
        # P(U|not c)P(not c) and P(U)P(not c) terms
        punotc_pnotc = punotc * (1 - pc) * math.log10((punotc * (1 - pc)) / (pu * (1 - pc)))
        punotc_pnotc += (1 - punotc) * (1 - pc) * math.log10(((1 - punotc) * (1 - pc)) / ((1 - pu) * (1 - pc)))
        return puc_pc + punotc_pnotc
# Example cases
if __name__ == "__main__":
        # Independent events: P(U|C) = P(U|¬C) = P(U)
        mi1 = calculate_mutual_information(0.5, 0.5, 0.5, 0.5)
        # Correlated events
        mi2 = calculate_mutual_information(0.5, 0.5, 0.8, 0.2)
        # C determines U (perfect correlation)
        mi3 = calculate_mutual_information(0.7, 0.7, 1.0, 0.0)
        # Realistic correlation
        mi4 = calculate_mutual_information(0.6, 0.4, 0.75, 0.5)

But does it work in practice?

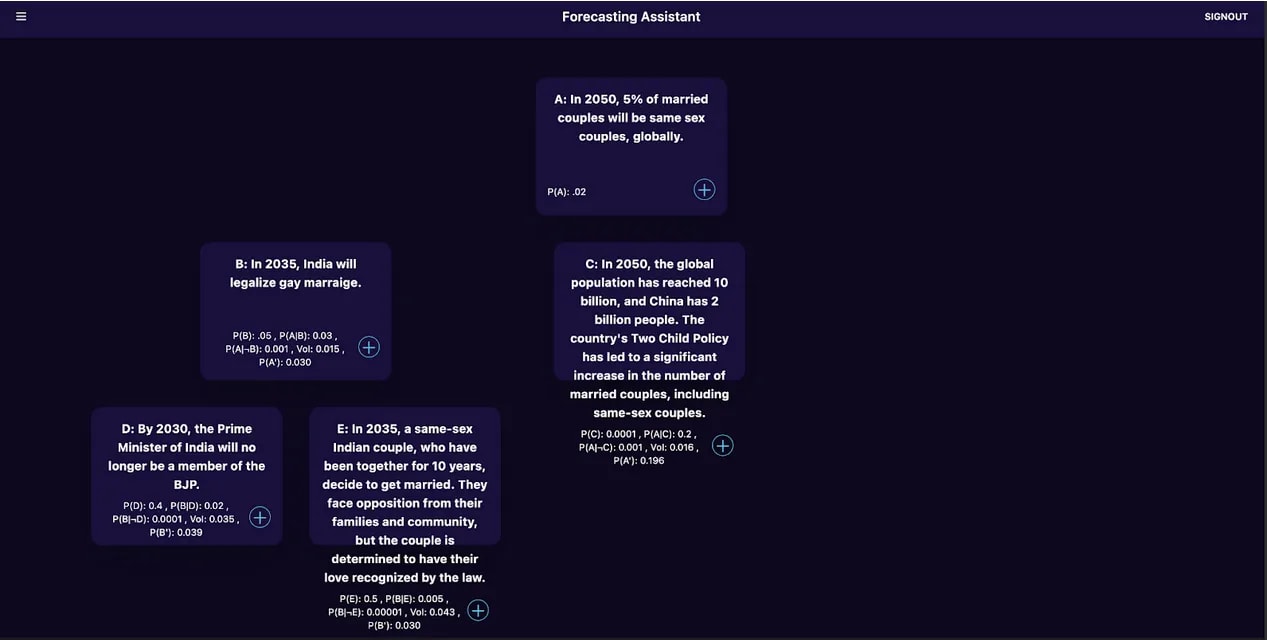
We test-drove the idea of trees for thinking better at Manifest 2023, a session called "Good Questions Tournament." Given a hard question like In 2050, what percentage of married couples will be same-sex couples, globally?, half the room generated intermediate/crux questions and half the room judged the questions by forecasting (we took the mutual information as described above). We had also finetuned GPT-3.5 to generate good crux questions to see how well these human assistants performed relative to the finetuned model. People judged each other's cruxes and the model-generated cruxes (without knowing which were which) and on average, the model's cruxes were judged more informative. Of course, this was a very small tournament! We would be very curious to see whether this holds up in more rigorous experiments.

If you want to experiment with these ideas, whether for expert forecast elicitation or for thinking through/parameterizing your own forecasting models, I might be interested in helping you! Feel free to DM me. We're currently experimenting with several reasoning models like this at Metaculus.

1. ^{^}

    Brier (quadratic) scores are bad. Another time, I'll write a tirade about this but if I'm honest Brier scores and log scores (aka Good scores, for I.J. Good, or ignorance scores if you're a meteorologist) aren't often that different in practice. A couple of things to read if you really love scoring rules: Brocker and Smith 2007 (there is only one proper, local score for probability forecasts); Du 2021 on the importance of being local, not just proper; Roulston and Smith 2002 (Evaluating Probabilistic Forecasts Using Information Theory — this is the one I always point to for why Brier is trash).

2. ^{^}

    "Relevant dominant uncertainty" is a concept introduced by Petersen and Smith in their paper Variations on Reliability: Connecting Climate Predictions to Climate Policy, which talks about different kinds of uncertainty and how to communicate model-based findings to decision-makers. "The RDU can be thought of as the most likely known unknown limiting our ability to make a more informative (perhaps narrower, perhaps wider, perhaps displaced) scientific probability distribution on some outcome of interest; perhaps preventing even the

   provision of a robust statement of subjective probabilities altogether." Highly recommend! Variations on Reliability: Connecting Climate Predictions to Climate Policy 

3. ^{^}

    Cunningham's Law - Meta