Subgame Purrrfection—Guest Writer Jaiveer Singh Explores Subgame-Perfect Nash Equilibrium
By Non-zero-sum James @ 2024-10-09T00:38 (+1)
This is a linkpost to https://nonzerosum.games/subgameperfection.html
NORMAL-FORM GAMES
Whenever you see the phrase “game theory”, the infamous prisoner’s dilemma example probably pops up in your mind; two prisoners, under interrogation, can either cooperate or defect to get an associated payoff.
As with most games that we study when first introduced to game theory, the prisoner’s dilemma is an example of a normal-form game-where players must act simultaneously in order to analyze their payoffs1. In the prisoner’s dilemma, if one player acted after the other, with knowledge of the first players’ actions, the second player would have a clear advantage. This change affects the Nash Equilibrium …
A Nash Equilibrium is a situation where no player can improve their payoff by unilaterally changing their strategy.
EXTENSIVE-FORM GAMES
On the other hand, extensive-form games, explore situations where there is a passage of time between decisions-decisions aren’t made simultaneously.
In perfect-information extensive-form games (which are what this piece analyzes), players have perfect knowledge of all past actions, both by themselves and their opponents, while making a decision2. Take chess-a player knows all of their opponent’s past moves and makes their decision accordingly. Another example of an extensive-form game is ultimatum bargaining, which I’ll use later to explain the concept of subgame perfection. But first we need to understand…
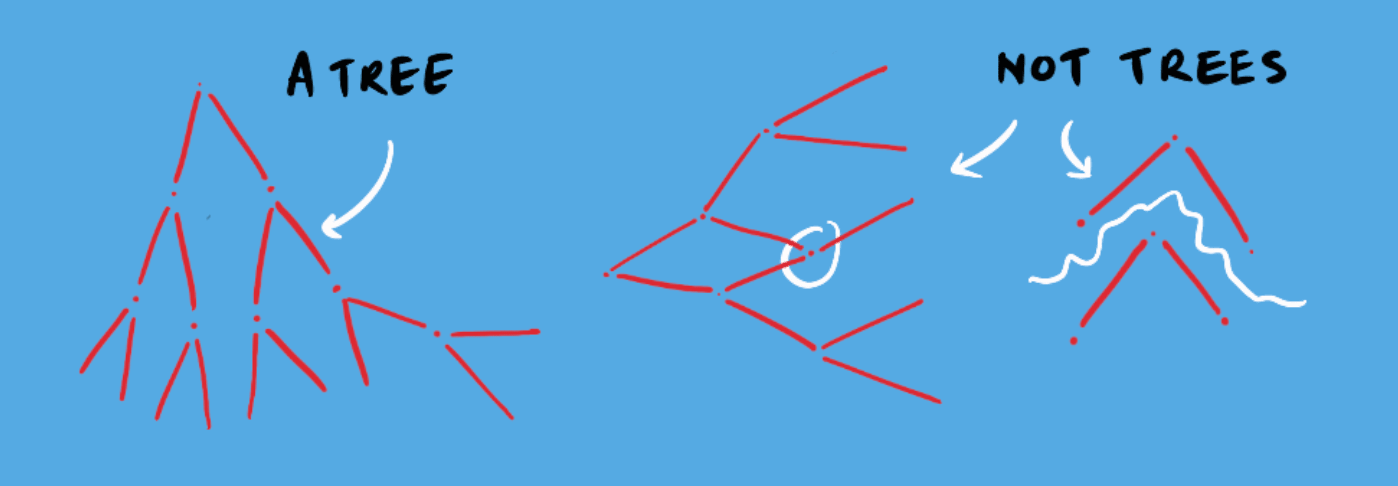
GAME TREES
In order to clearly represent the sequence of decisions by participating players, their options, the associated payoffs, as well as the information available, we use game trees3. Nodes make up these trees, with each node representing a point where a decision has to be made. Each node further branches out, showing the outcomes associated with decisions made, as shown below:
SUBGAME PERFECTION
Having understood extensive-form games and their representation through game trees, we can now proceed to subgame-perfect Nash Equilibriums.
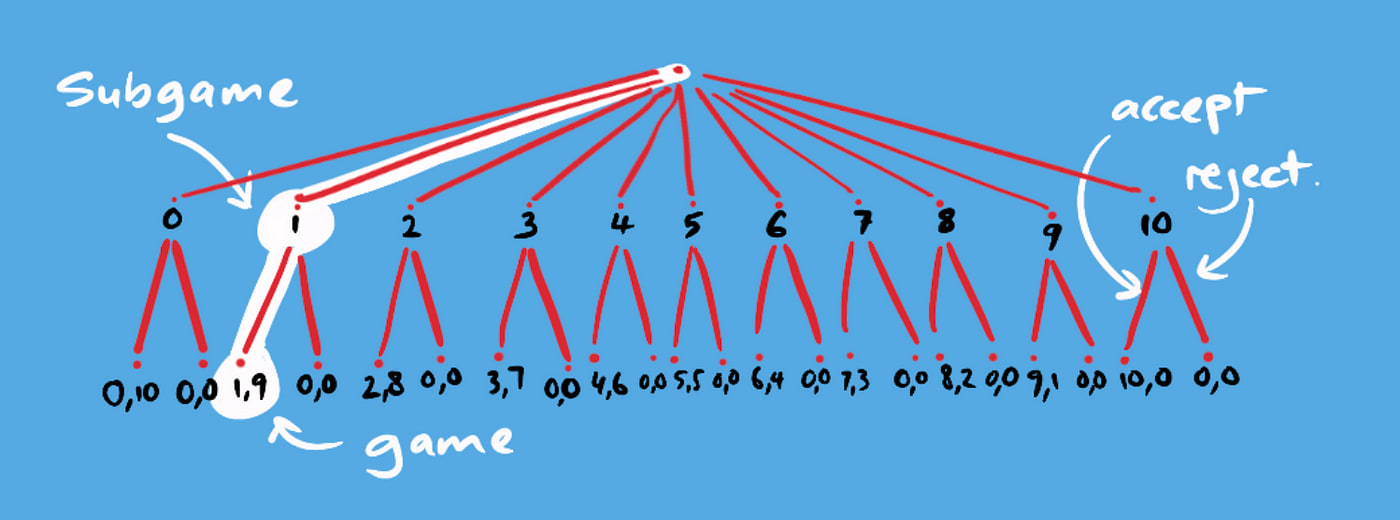
A subgame-perfect Nash Equilibrium occurs in an extensive-form game when each individual node or subgame represents a Nash Equilibrium4. In other words, each player’s decision at an individual node can be thought of as a subgame and their best response considered a Nash Equilibrium of that subgame. When this holds true for all subgames and the overall outcome, the Nash Equilibrium is said to be subgame-perfect.
ULTIMATUM GAME
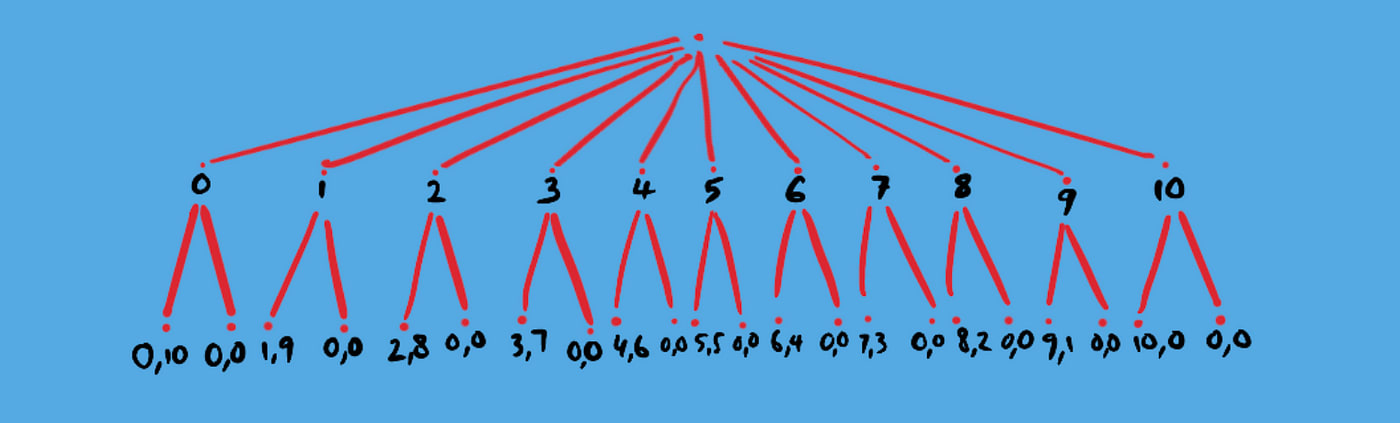
Imagine you are given $10. To keep the money, you have to give a portion of this $10 away to another player. Sounds simple enough. Give the other player as little as possible. The catch is, if the other player rejects your offer, you both get nothing. This is the Ultimatum Game, a form of take-it-or-leave-it bargaining.
In the image, the first node shows the eleven options available to player 1 and the subsequent 2 branches at each of the eleven second row nodes show player 2’s available decisions with the associated payoffs (player 2 payoff, player 1 payoff). What would you do as player 1?
Assuming player 2 is perfectly rational and aiming to maximise their own payoff, the right offer to make is never more than $1.
Why? Looking at each of player 2’s payoffs, ignoring the total sum of money and fairness, it is always a best response to accept any offer more than zero. Is this a subgame-perfect Nash Equilibrium? You get $9! Player 2 gets only $1. The answer is yes, it is subgame perfect, because player 2 is playing a rational best response in their individual subgame, with only 2 possible outcomes: 0 and 1.
BEHAVIOURAL IDEAS
Does this really happen? Let’s change the scenario. Put yourself in player 2’s shoes-would you accept $1, when the other gets $9, even though a dollar is better than none? According to a study by Haselhuhn & Mellers, conducted on business students, around 75–80% of participants rejected an offer of $1. Almost no one rejected an offer of $5, but some even rejected an offer of the full $10!
Turns out most people aren’t the perfectly rational, self-interested “homo economicus” that game theorists and economists might assume. Normative ideas of fairness and social preferences permeate through real people’s decisions, especially in repeated games. If the situation above is iterated, then the strategy profiles change, even for perfectly rational individuals. If player 2 repeatedly rejects unfair offers, player one may alter their strategy to avoid future “punishment”. Player 1, now analyzing their average payoff over a number of games, may be willing to offer a higher amount.
SO…
In the Ultimatum Game, subgame perfection holds that Player 1 offers the smallest amount, and Player 2 accepts, to avoid getting nothing. However, in iterated games, considering the opponent’s interests becomes a rational part of a player’s self-interest, much like in real life.
RELATED MATERIAL
- It’s interesting to note that, in order to apply “rational” behaviour to the Ultimatum Game, a player needs to view winnings in absoluteterms rather than relative (they’re trying to maximise their payoff, not “win” relative to the other player). You can read about this more in Relative Gains — how not to measure success
- To explore more about how notions of fairness and cooperation arise, read Andrew Tane Glen’s Why Cooperate which introduces the idea of the ‘super-defector’.
- You can also explore Nash Equilibrium.
- Game Theory Online — GTO-4–03: Perfect Information Extensive Forminformed the explanation of Nash Equilibrium in the context of perfect information games.
REFERENCES
- Dekel, E., & Siniscalchi, M. (2015). Epistemic Game Theory was used to provide a foundation on the simultaneous action and payoff structure of normal-form games.
- The definition of extensive-form games comes from Game Theory: Key Terms — Economics for Everyone, which outlines how players have perfect knowledge of past actions in these games.
- Chapter 3 Representation of Games was used to explain how game trees are used to represent the decisions in extensive-form games, this informed tree diagram illustration.
- The formal definition of subgame perfection can be found in Subgame Perfect Equilibrium — an Overview.
- The Ultimatum Game tree diagram was adapted from Schuster, S. (2017). A New Solution Concept for the Ultimatum Game Leading to the Golden Ratio.
- Behavioral studies, such as Haselhuhn, M. P., & Mellers, B. A. (2005). Emotions and Cooperation in Economic Games, were used to illustrate how real-world decision-making often deviates from theoretical predictions.
Originally published at https://nonzerosum.games.
SummaryBot @ 2024-10-09T12:46 (+1)
Executive summary: Subgame-perfect Nash Equilibrium in extensive-form games requires rational best responses at each decision point, but real-world behavior often deviates due to fairness considerations and social preferences.
Key points:
- Normal-form games involve simultaneous decisions, while extensive-form games have sequential decisions represented by game trees.
- Subgame-perfect Nash Equilibrium occurs when each decision point (subgame) represents a Nash Equilibrium.
- The Ultimatum Game illustrates subgame perfection, with a theoretical optimal strategy of offering the smallest amount possible.
- Behavioral studies show people often reject unfair offers, contradicting purely rational self-interest assumptions.
- In repeated games, considering opponents' interests becomes part of rational self-interest, leading to fairer offers.
- Understanding subgame perfection requires viewing payoffs in absolute rather than relative terms.
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.