Phil Trammell on Economic Growth Under Transformative AI
By Michaël Trazzi @ 2021-10-24T18:10 (+10)
This is a linkpost to https://youtu.be/2GCNmmDrRsk
This is a transcript with slides for the latest episode (audio, youtube) of "The Inside View", a podcast I host about the future of AI progress. I interview Phil Trammell, an Oxford PhD student in economics and research associate at the Global Priorities Institute. Phil was my roommate and last time I called him he casually said that he had written a literature review on the econ of transformative AI. A few weeks ago, I decided that I would read that report and translate what I learn along the way to diagrams.

Michael: thanks for being at the podcast, it's been a few months since we've wanted to do this. Today we're going to be talking about the paper you published on the GPI website a year ago called "Economic Growth under Transformative AI". That's a paper you co-wrote. Can you tell the audience a bit about what is this GPI, for those who don't know, and what you do there
Phil: right so GPI is an institute at Oxford doing research in philosophy and economics, mainly economic theory, at least at the moment, relevant to people who want to do the most good. So philanthropists in the EA community would be a sort of obvious audience. I'm an econ PhD student at Oxford and I'm sort of being sponsored by GPI and I work part-time at GPI... but mainly my work just overlaps with GPI's goals. So the econ research I do as a grad student is the sort of work that GPI wants done. I sometimes do kind of outreach and so on through GPI but mainly the two hats just sort of overlap. And one of the things I did in my capacity is an econ researcher, which is now on the GPI website as you just mentioned, is this literature review. It's not really an original paper but a synthesis of work that has been done over the past few years on AI and economic growth.
Michael: and that's perfect because the podcast is about AI, so people I think will be kind of familiar with AI or AGI, or those concepts, maybe not with transformative AI if they are not effective altruists, so could you maybe define what you mean by "transformative AI" in this paper?
Phil: people have used that term in slightly different ways. What I mean by it is AI that has a transformative effect, and I'll define that in a moment, on the economic growth rate, the wage rate (growth could stay the same but people's wages could fall a lot or something so that would be different) or the labor share. And the labor share is the fraction of output that gets received in exchange for labor, that's received as wages, as opposed to as capital rent, so it's interest on investment. Historically, for a long time now, even if a thousand things have changed about the economy, about two-thirds of output has gone to labor, being paid out as wages. Hopefully that makes sense, like on average people's income two-thirds of it comes from from their job as opposed to from their investments, and one-third is from investments and that could change a lot if AI takes off in a big enough way. So those are the three things that could be transformed... transformed by AI, for AI to be transformative on my account. Ok, so what do I mean by transform? It could... if a variable that's been constant for a long time falls to zero, I call that a transformative event (so like the labor share falls to zero). If a growth rate stays constant... so economic growth say, or wages, have been going up at like a few percent a year for a long time: if that falls to zero, that's transformative. Or if the growth rate significantly increases, so if it rises to like 40 percent... Or if it starts increasing without bound, so if instead of jumping as a one-off event it goes from two percent to forty percent, that would be the previous sort of transformation I mentioned, but it could also be transformative if it just rises without bound—it goes from two percent this week to four and then 100 years later it's like way higher, it's rising still, and the most radical sort of transformation would be if one of these growth rates... if the economic growth rate or the wage growth rate exhibit a singularity. This is where it sort of looks like it's going to infinite output in finite time. The one caveat I'll say is that, that doesn't need to happen literally for the event to qualify as transformative it just needs to follow that path for a while if it looks like it's approaching... it's a growth rate... if output seems like it's going to a vertical asymptote but then it sort of starts flattening off in a long time once we run out of atoms in the universe or something then it still counts as transformative.
Michael: so if we if we have the growth rate that doubles after a year and then it doubles after six months and three months, and a month and a half, we could still consider it to be transformative.
Phil: yeah right if it keeps that up for enough iterations that it just feels like a pretty wild event... I don't have like a precise definition of how far it has to be maintained.
Michael: I think the your your point about the growth rate going to zero being transformative is original. I didn't understand it like that... I thought it was the other cases that was kind of transformative, but imagine AI resulting in some kind of war and we have no more growth... would that still count as transformative?
Phil: I think that's... it's not a really practical issue when it comes to a literature review because... none of the papers on growth theory under transformative AI have taken that scenario seriously. It just doesn't show up on the tables. But I do think that would be a transformation to the world. If AI like kills everyone and then there's no growth I think that, you know, that's a transformation.
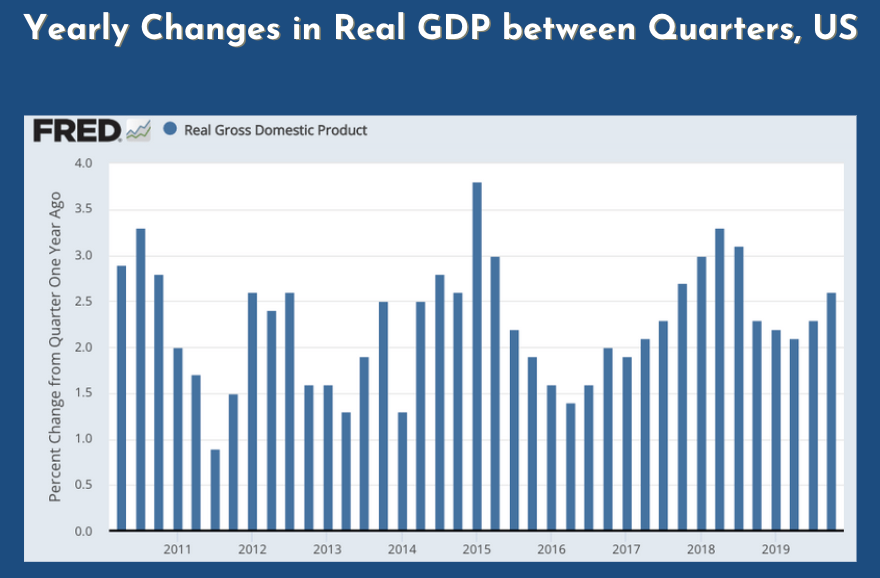
Michael: Definitely. I think for people who don't have an econ background, we keep talking about growth, growth rate, etc, but we might want to define those basic terms like GDP or growth rate or those things precisely. I think the next slides are exactly about that. I just put that on so that you could explain what we mean by two to four percent. I removed the recessions so we have something fairly stable between 2011 and 2020 where we just look at the difference in GDP between two quarters... sorry two years for the same quarter. Could you explain maybe like what's GDP briefly, without going too much into details?
Phil: sure so it's just the the quantity of every good or service that that was sold over the past year... well of every final... every consumption good or service... times the price that it's sold for. So you just think of all the haircuts that were given times the cost of the haircuts and all the cars that were sold times the cost of each car. You don't you to count all the parts like... if the car was made of different... by a bunch of different manufacturers you don't want that would be sort of double counting but you just count the consumptions
Michael: you don't call the intermediary products like the eggs to make cakes but only the cake
Phil: that's right, unless the cake was made in the home in which case that's
Michael: in here the title is the real GDP and when we say real GDP we we take a fixed prices like. I think people use the dollar US dollar from 1990s or 2000s... they'reach fairly common.
Phil: right, because when there's inflation you don't want to say that GDP is rising... or when this deflation you don't want to say that it's falling. You want this measure to track the real increases or decreases to haircuts and intakes and cars... so you just pick the prices from one year and then you kind of use the others to track.
Michael: how do you do when... imagine Tesla invents a new car, how do you count the price in the previous dollars?
Phil: right so there's different ways of trying to do that... you can say "of the goods that were around last year, how many of them are people apparently indifferent between one Tesla and many of the old things?". Like let's say people are indifferent between having one Tesla and two old Ford cars from last year, and then this year a bunch of Teslas are sold and we can count them each as being ford cars. Now, that doesn't actually work. So, if you really take that idea seriously, I think you went into all sorts of logical inconsistencies and for the most part we just sort of freed them under the rug but when you're... especially when you're comparing GDP levels over long time horizons where lots and lots of the products available at the end were not available at the beginning, it might not be possible to do this sort of reasoning because there might be no quantity of the goods available at the beginning that people would trade for some of the goods available at the end. If you could only have a grain and olives and whatever the ancient romans had... stone, it might be that even an instant amount of that stuff would not be worth having instead of one car or one nice modern house with air conditioning so...) I actually have a paper (link) I've been working on that tries to kind of come up with a sort of alternative framework for thinking about rises in output over time, which you can link to if anyone's interested. But anyway, over short periods, then you can kind of wave your hands and do what I said and say "okay well maybe one Tesla 's worth two Fords"
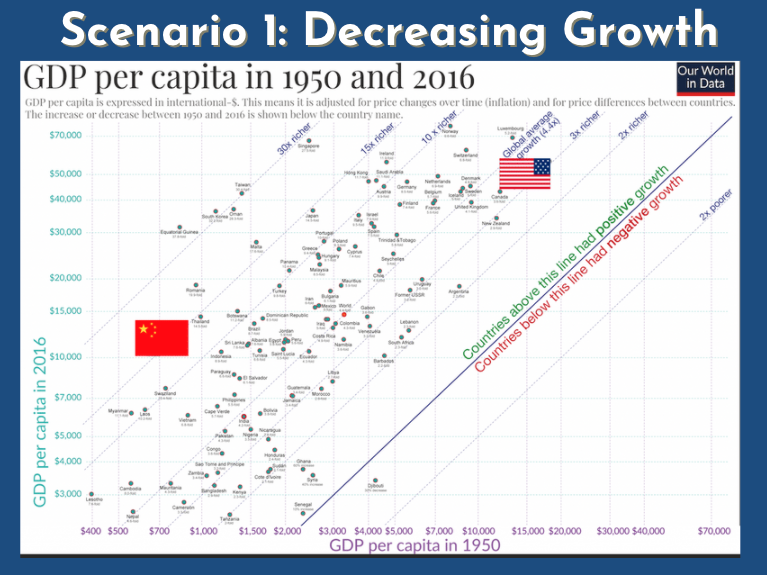
Michael: I'll be happy to link it when it's published... and I think the next, so the next slide gives the different scenarios. In this slide we see the growth rate... the GDP per capita for different countries between 2016 and the 1950s, and you see that the global average growth is at 4.4 between those two times, and the US is a little bit less... so between 3 and 4.4 and Chine is at more than 15 times richer than it was in the 1950s. So in some sense we could say that developing countries have a huge growth and then they go and have a decreasing growth rate until they reach the growth rate of developed countries. Would you agree with that statement?
Phil: I'd say that when you're not very developed, and in particular when you haven't yet adopted the technologies that more developed countries have, then you can grow just by accumulating capital, just by piling up all these new sorts of factories that... you haven't been making use of so far. So you can exhibit what's called "catch-up growth". Developing countries don't all exhibit catch-up growth. You also need the right institutions and so on to allow for all that capital accumulation. But it can allow for it. And that that does seem to be what's happened in Chine and then once you reach the technological frontier you'll have to slow down until you're just growing at basically at the rate of technological progress... something like that.
Michael: we've reached those kind of levels of growth rates since the Industrial Revolution. So there was like some kind of permanent increase since the agricultural and industrial revolution. Do you want to talk a bit about that? I have a graph from year one to year 2018... do you want to explain a bit how that happened?
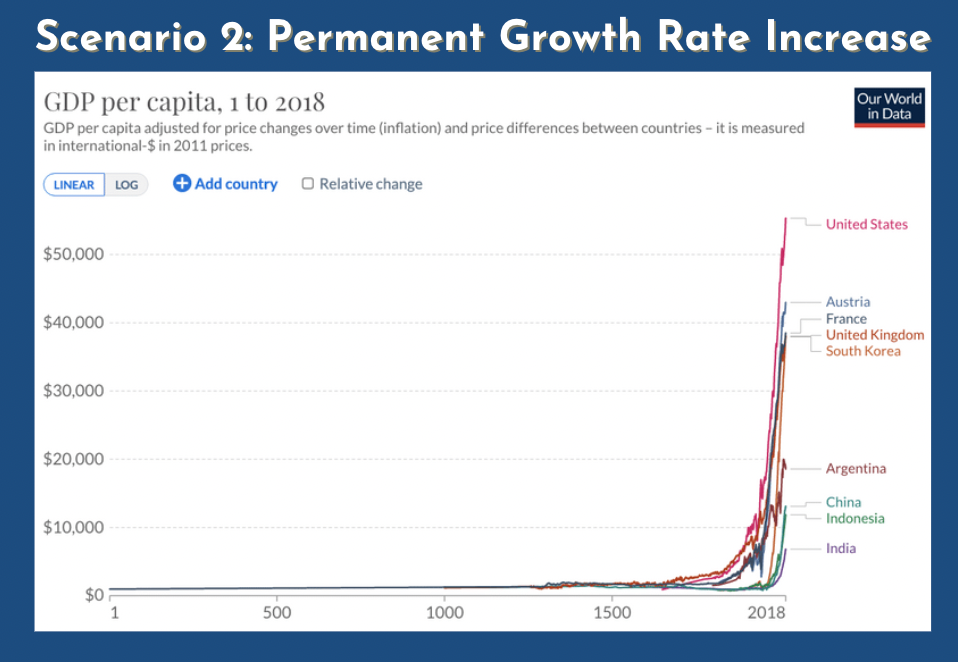
Phil: so... for a long time basically until the, I don't know, 1700s or something... depending on where... or 1800s depending on where you draw the line. The world was at pretty stagnant GDP per capita (it was just a bit above subsistence so the population... when output grew if you developed a new method for farming to create more calories per hectar of land, population would just grow and GDP would grow, but GDP per capita would stay about the same). It wasn't quite that bad but it was... it was something kind of like that. So GDP per capita stayed about flat... Then, for reasons that are still very much being debated, and basically in North-Western Europe, the growth rate really took off, and instead of being next to nothing, it rose to something like two percent per year. (This is a growth rate in GDP per capita). And that's made such a difference that as you can see on this graph it's just almost incomparable to what has been going on for the past few centuries compared to what it was before them.
Michael: this was because of technological progress in the steam engine, railroad and so it makes sense that if we build again more transformative technologies such as self-improving AI or even automation of human labor we could see something similar because the steam engine automated some of human labor at some point as well.
Phil: right, so when I said it's not clear why this happened, I guess I mean it's not clear why people went from not developing new technologies to developing them very fast. But everyone would agree that technological progress was approximately a cause of the industrial revolution and that a good way to model... a good way to think about the way in which technology allowed for this explosion in growth, is at least in large part that it allowed capital to better substitute for labor. So we could now have this stuff that we can just accumulate, we can just pile up, without raising the population that is factories and so on... do some tasks that formerly had needed human minds and hands, so we could have more output per capita, yeah.
Michael: so that's the second scenario that you outline is... if we had a similar increase in the growth rate as the Industrial Revolution in the future, that could be transformative.
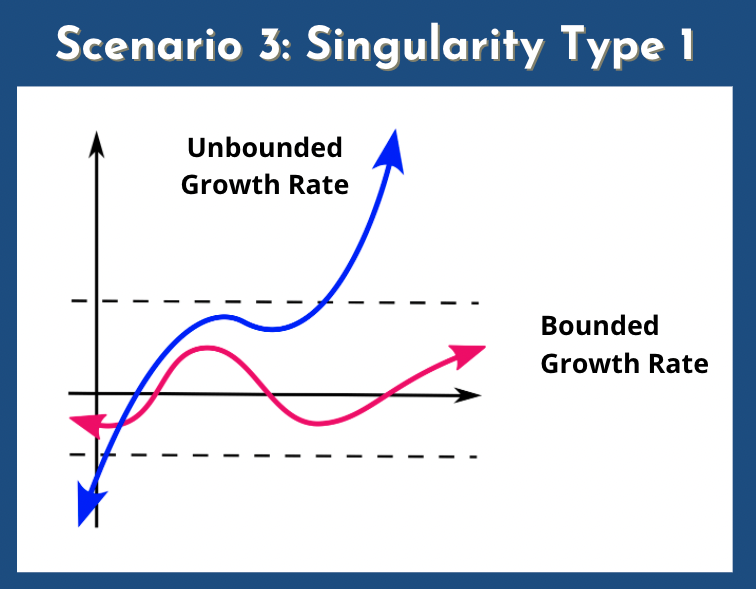
Michael: But an even more even more drastic change is a singularity of type I where the growth rate doesn't have an upper bound and keeps growing. I think you already mentioned that but if you want to talk more about that you can go for it.
Phil: so I decided that there are three ways the growth rate could rise in a way that was like significant enough to call it transformative. The first was a significant one-off increase to the growth rate, let's say growth rate of GDP per capita. Okay, so that could rise from, say, two percent a year, to something much higher. It could start rising itself without bound, so this is... I did call it a type I... I don't think it was called a type I singularity at the time... but this is what is sometimes known as, or it could exhibit a type II singularity, which is like a true mathematical singularity, where it doesn't just go to infinity, but it goes to infinity in finite time, and this seems kind of crazy, but I should maybe remind everyone that like, even constant growth is crazy, indefinitely. In fact, even constant output is crazy. Like if you really think that it'll last forever you can't have just output at the current rate past the end of the universe—all of these scenarios are only for a while. And, yeah, the idea of a type II singularity is just that we follow a curve that resembles this curve that's on the side here until we start reaching some plateau that that's governed by dynamics outside of this model but but sorry so so about that first possibility that there's just a one-off increase to the growth rate that has to be a big enough increase to count as transformative, and I haven't said anything about how big it would have to be if we have one of the two kinds of singularities. It doesn't matter where you draw the line, thirty percent growth per year, fifty percent, whatever. We'll cross it eventually if we take this curve literally. This curve or the the type I curve but if we're talking about a one-off growth rate increase, we want to distinguish between an increase that's just like going... it goes from two percent to two point one percent or three to three point one. Well distinguish that from something that really makes the world feel different. One way of drawing that line people have sometimes used is to say "we'll call it transformative if the proportional growth rate increase due to AI is as big as, or bigger than the proportional growth rate increase induced by the industrial revolution". I said it was basically flat (there was basically no growth in output per capita before the industrial revolution). Well that's not quite true. People sometimes estimate it was around point one percent per year at the time, and then it was like two percent per year afterwards, so that's a multiple of 20. Another multiple of 20 would be 40 growth per year so that might be a natural place to draw the line. I think that's a bit high because even if we had like 39 percent growth a year that would still feel pretty wild and maybe I'd draw it in the teens somewhere. Like maybe if we have like 12 percent or 15 percent growth then that's far enough outside the historical norm that should count as transformative.
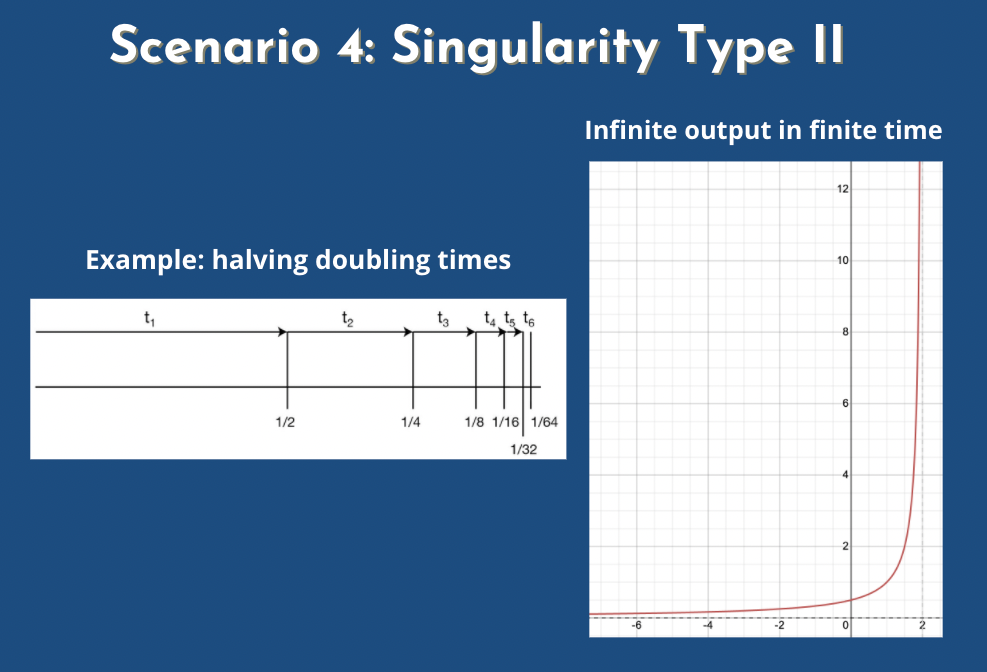
Michael: people often talk about the doubling time in GDP... if the doubling time in GDP is something like a year right?
Phil: that would be drawing the line even higher.
Michael: we've been through all those scenarios. I think we are going to go through them even more in the next slides, but we can maybe start with defining the basics of the models you use for your paper which is capital, labor and output.
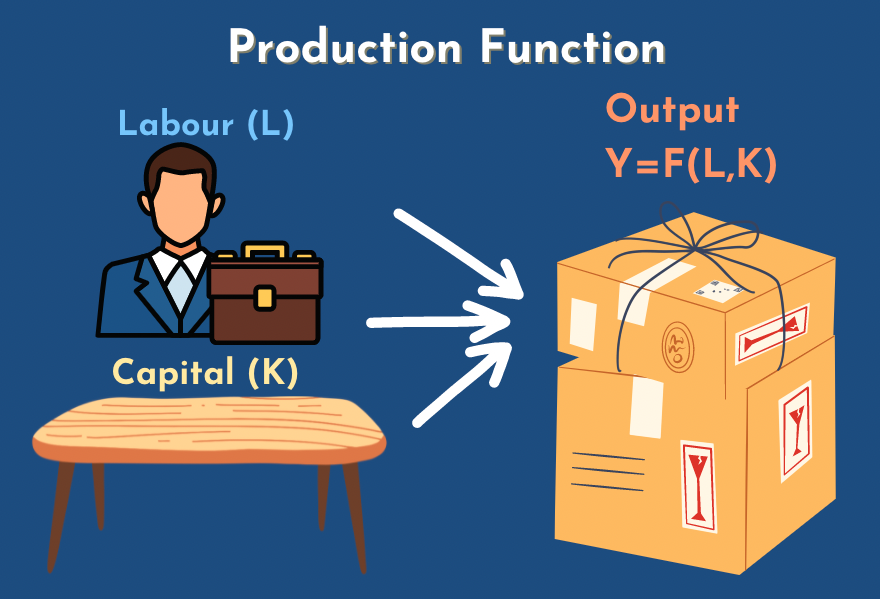
Phil: We were talking about GDP before, all those cars and haircuts and so on. Where do they come from?
Michael: from desks?
Phil: well, some of them come from a desk. I'm at a desk now. They use a lot of inputs but we can divide them into two categories labor and capital where labor is obviously human input and capital is desks and factories, and the scissors that the barber uses and all of that, and we have a function, F there, which takes in all the labor and all the capital and spits out output, GDP.

Phil: So you can think of it as like the whole economy is just a big factory with two big tubes going in, the worker limbs and the desks and metal and everything and then the outcome is GDP.
Michael: it's a bit apocalyptic to have humans in tubes... but I get the idea.
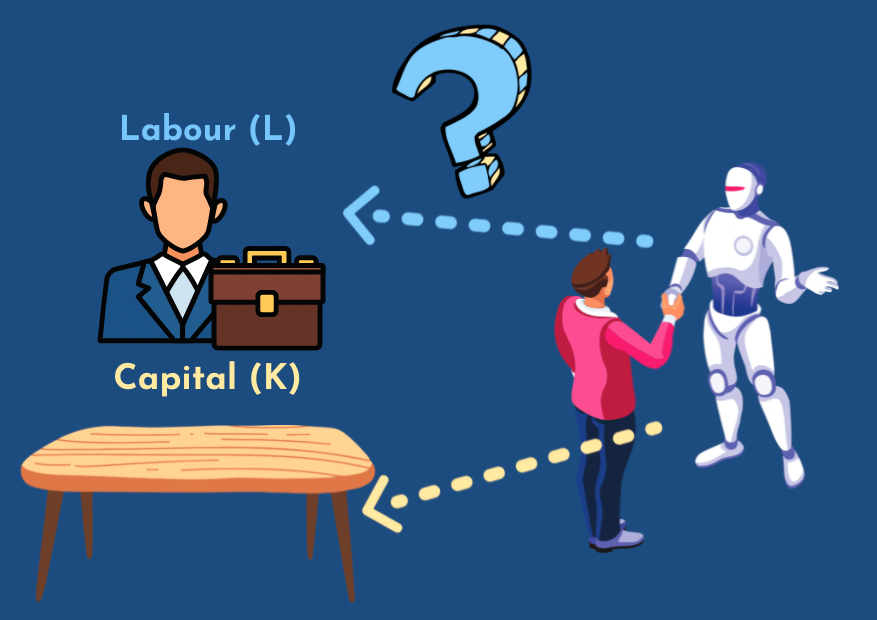
Michael: To go back to AI, if AI automates labor and like start to think like humans and does work like humans, we want maybe to consider them labor. And if we're just like building more computers they're more obviously capitals. If they're like servers or so... I guess then the distinction between those two is less thick for AI.
Phil: I agree.
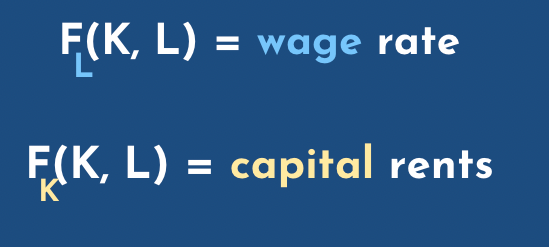
Michael: so let's go further, so for for this I guess I just try to... the little L and K are your notation, which is just a derivative... the partial derivative for the labor and for capital and I guess that's if we're assuming that we're paying people their marginal products. So could you define what's a marginal product?
Phil: hum, sure. The marginal product of a worker is the extent to which output increases holding everything else the same when that worker puts in another hour of work or the amount it falls when they put in an hour less work... not an hour, an infinite decimal amount, but let's say an hour. And in a world with competitive markets, as they're called, the workers hourly wage should be their marginal product per hour in this sense. Why? Well, because if you've got, say, factories around or you have barber shops around, if a given factory or barbershop or whatever isn't paying someone their marginal product then they can just go to a similar one across town and say: "pay me a bit more" and they'll be willing to do so. Things don't always work out that neatly but I think it's a good place to start. So that's the marginal product of labor and why you should expect it to be the wage. By the same token, the interest rate should be the marginal product of capital, so the annual interest rate. Should be, let's say, I have some some equipment that can be used in a factory or has some scissors or something and I lend them... I lend it to the... let's say it's scissors. I lend them to a barber shop. how much...
Michael: very nice of you
Phil: well but I'm going to get paid
Michael: oh yeah
Phil: How much am I going to get paid? The extent to which they they're able to make more money over the next year because they have an extra pair of scissors and so that's the marginal product of capital and that should be the capital rental rate or the interest rate, same thing.
Michael: yeah, so I guess more interestingly is when you start to insert technology into that, and so
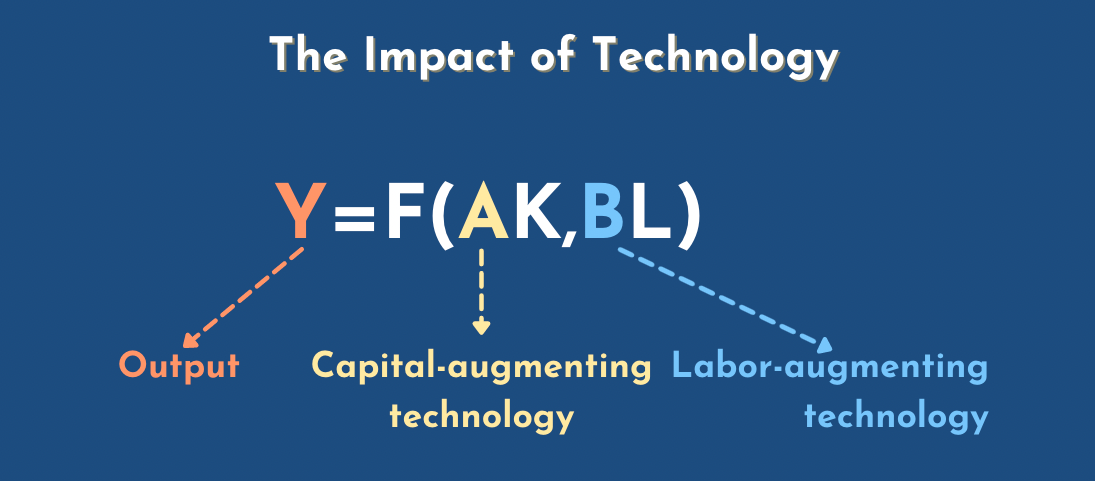
Michael: you can either have multipliers for capital, capital augmenting technology or multipliers for labor, labor augmenting technology. How do you distinguish those two individually?
Phi: let's say we come up with a way to re-organize the factory—the metaphorical big factory of the economy which has two tubes going in and it has one tube coming out.

Phil: We reorganize it so that the same amount of output comes out the other end if we use half as much capital going in as before let's say. So you still need to put in the same amount of same amount of bodies but now you can just put in half as many screws and scissors and stuff and the same output comes out as before. Then, that's what we'll call a doubling to A, the capital augmenting technology. A doubling, does that make sense? Because now you only need half as much K to get the same Y, holding the B and L constant.
Michael: But this technology is still a bit surprising: how could we need half less screws?
Phil: oh well this happens all the time it takes a lot less metal now to make a car than it used to back in Ford's day.

Phil: Somehow we've come up with ways to to just shape the structure things... shape the car itself so that the the pieces can all be thinner and lighter and not use as much metal and that's also good for gas efficiency.
Michael: I think for production of materials, or for cars... for products it's quite easy to measure it, I think, in your paper you mentioned that to measure technological development in general, sometimes it's very easy... it tends to be very hard because you can really have like very long-term repercussions. Like I think you said "the importance of the atomic bomb is not well approximated by the cost of the Manhattan project". When you were writing this, what were you thinking about the other consequences or externalities of the atomic bomb?
Phil: naively you might say: "how important (in some economic sense) is a given technological advance?". Well, that's not naive, that's a reasonable question. A naive thing would be to then, say, well, it's going to be reflected in how much people were willing to pay to develop it. So if you've got car companies and they're making their cars and they... you see... that they don't just spend on steel and on workers to put the steel into shape to make a car, but they also hire some engineers to think about how to make the same car with less metal, you might say "well how important is this new design that saved some money when making the car". Well, we can just say, well, how much were they willing to spend on engineers to come up with this?
Phil: That should be something like how much they saved, because if they're saving more than then they spent on the engineers then, yeah, it's sort of like, they have some market power. They could have invested in even more engineers, and they probably would have been saving more money on that margin, so, at first glance, you might think "okay the value of the invention is something at least for those sort of marginal inventions... for things that the company was just indifferent between funding and not funding, those are the ones where the cost is about the same as the extent to which it actually increases output" but for all kinds of technological advances their impacts are not captured by the people funding them.
Phil: They have lots of impacts on the world, and so those impacts are many steps removed from the organization, or individual deciding how much to spend on it. And then they might be totally unforeseeable, and have ramifications to the generations. And it would just be silly to use this framework very widely, and, as an extreme example in which that sort of framework would break down, you can consider the Manhattan project which introduced atomic weapons to the world. And I don't know how much the US government spent on the Manhattan project, but it's not... you can say that if you're trying to figure out what are the most important ways in which atomic weapons change the world, looking into how much Einstein got paid, it's not going to be... not that much compared to the value of winning a war.
Michael: and, I guess, when I ask you to distinguish the two, it's because when I try to think about what AI could bring, or the internet, or when you people use emails or slack and build new servers, new software, they're kind of things that... they can make computers go faster, and more efficient, and they can also make so... if my computer is more... is faster, the human using the computer will also be more efficient so it will be a labor augmenting technology. In some sense if we have some innovation that enables to make all the computers twice faster, it would both make capital and labor hum, better off, I believe.
Phil: well, there is a difference between making a certain factor, or its owners, better off, and making it more productive. In fact, if this production function F here... if for F, capital and labor are what are called gross complements, meaning that basically you really... if you have a lot of one thing you don't really need any more of that thing you just need the other thing.It's left shoes and right shoes. That's how capital and labor are. Then making a certain factor more productive is bad for the owners of that factor, and making the other factor more productive is good, so if you've got a factory, and you've got machines and people, and you need one person for a machine, and then you suddenly come up with labor augmenting technology, that now means you only need half as many people. You come up with a new training, say for... so the workers can operate twice as many machines at once, then you can just fire half the workers and what happens to the wage? Well it goes way down because no one's really all that necessary you've got this sort...
Michael: you're saying that there's some kind of interaction between those two where if one becomes more productive, or efficient, then you can just remove the other one or remove half of it?
Phil: yeah, so that's in a static setting. Now, when you really think things through, then you have to say well, hold on, if we have all these extra workers lying around, and we can pile up the capital, well at the moment, maybe wages, will go down, but in time we'll end up with twice as many factories as we had before. Because that, well, we'll just accumulate capital and we'll be able to make money. We'll be able to make out... building new factories and hiring all these people that became unemployed, and at the end of that process people's wages should be higher. They should be twice as high in this case because each one of their marginal product will be twice as high, because if they leave now, two machines will be unused, instead of only one, but you just have to be careful between that example you gave about computers going twice as fast. I think if that's all that happens and nothing else changes, but computers get twice as fast, that's a case of capital augmenting technology not labor augmenting technology. But it might often lead to a rearrangement of work processes or production processes that amounts to labor augmenting technology, but in itself it's just capital augmenting technology, even if it makes workers better off because now they can get more done, that's a capital complementing their work.
Michael: it's as having a bigger desk, making people working on the desk better workers... so I think I didn't put all the conditions but, yeah.
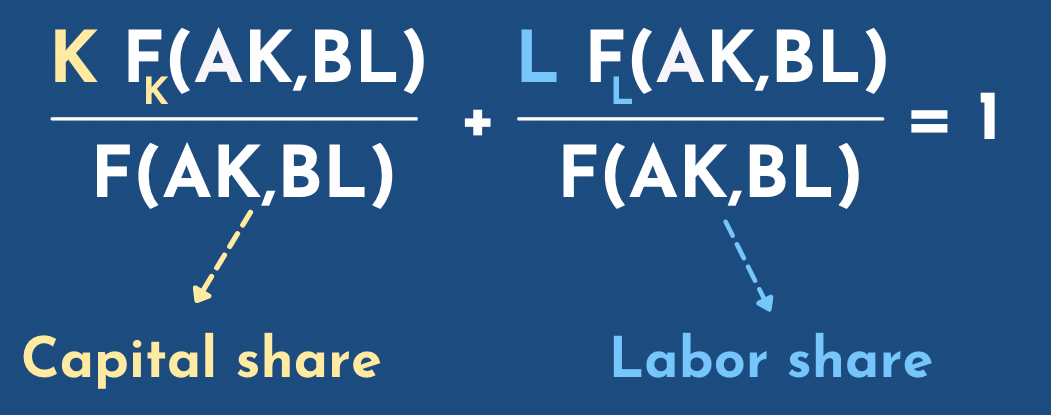
Michael:You already mentioned the wages and capital rents, but another terms are capital share and labor share, which we would also say if they go down or up in our scenarios... and there are certain assumptions that maybe we should not mention because they're mathematical assumptions. We get that those two sum to one. Do you want to explain this formula?
Phil: sure. So we said that each unit of capital got paid by its owner the marginal product of capital each year. Let's say, if we're thinking on a yearly scale, so that's that F sub K thing... it is a marginal product of capital and you multiply that by K the amount of capital and you get that the total amount that all the all the investors took home that year. And then you divide that by F of AK and BL... you divide that by the output, and you get the fraction of total output that got taken home as interest on investments. And then by the same logic, you think about, you know, F sub L: that's the the marginal product of labor, that's the wage, multiply that by L, the amount of labor, that's the total amount that workers take home as wages, divide that by the output and then you get the fraction of output that got taken home as wages, so if nothing's too screwy, those two things should add up to one. 100 percent of all of output got taken home either as capital capital rents or as wages, and in practice I just said the ratio has been about two-thirds.
Michael: and this has been consistent for the last century or something?
Phil: I think more, but the data gets worse the further back you go. But at least for the last century or so. And in recent decades, the labor share has fallen a little bit now. Maybe it's not... instead of being 67 percent now maybe it's 62 percent in the US and UK, and people make a very big deal about this, blame it on Reagan or something, but I think it's... I think the more striking fact is just that it's managed to stay so roughly constant for such a long time, even as the economy has grown a lot and industries have risen and fallen, and yeah...
Michael: and maybe with AI we'll be automating some part of this labor share, and it will shrink a bit, which is in all the scenarios you you will consider further on. We'll see if the labor share stays constant or goes down a lot, or even shrinks to zero.
Michael: Yeah so I think another concept that is central to this literature review is elasticity of substitution, and maybe to understand that... this took me a little some time to understand, so if someone has never... maybe have never heard of elasticity in general for normal products... and maybe you could start with that.
Phil: sure, so the elasticity of one variable with respect to another variable is the percent that the first one rises when the other one rises by an increment. If you're thinking about the price elasticity of demand for some apple, what you're asking is when the price of apples rises by a tiny tiny bit, it rises by a penny ...
Michael: I don't really look at the prices of apples.
Phil: Well but, okay, but you would if they if they got way higher, probably, if it was five times higher and there's someone out there for whom the current price is five times higher than the amount that it used to be in the amount they would be willing to casually buy them at... so there aren't going to be many people who stop buying apples or many apples they refrain from buying when the price goes up by a penny but the question is well let's say, a pound of apples is two dollars, so it goes up by a penny, so that's half a percent, to what extent does the quantity of apple's produced fall, if it falls by half a percent? Then the elasticity is one if it falls by one percent. That allows that the price elasticity of demand for apples is two.. so that's that's the idea and...
Michael: could you give examples of products that are like clearly elastic or where the price elasticity of demand is elastic, and or inelastic, so we have concrete real-world examples?
Phil: Sure, so how about some particular kind of apple? This is always... it's a always a little arbitrary, what you count as a good and what you count as a category of goods, but let's say we're just thinking about pink lady apples. I'd be very surprised if the price elasticity of demand for those were not well above one, because there are very close substitutes, right? On the shelf next to it, so people...
Michael: I guess one intuition for that is when the the price elasticity of demand is high then, if the prices changes people will just go for the substitute and they don't really care about this pink lady apple or something.
Phil: sure.
Michael: and how do you translate this concept to, you know, capital and labor, and this elasticity of substitution.
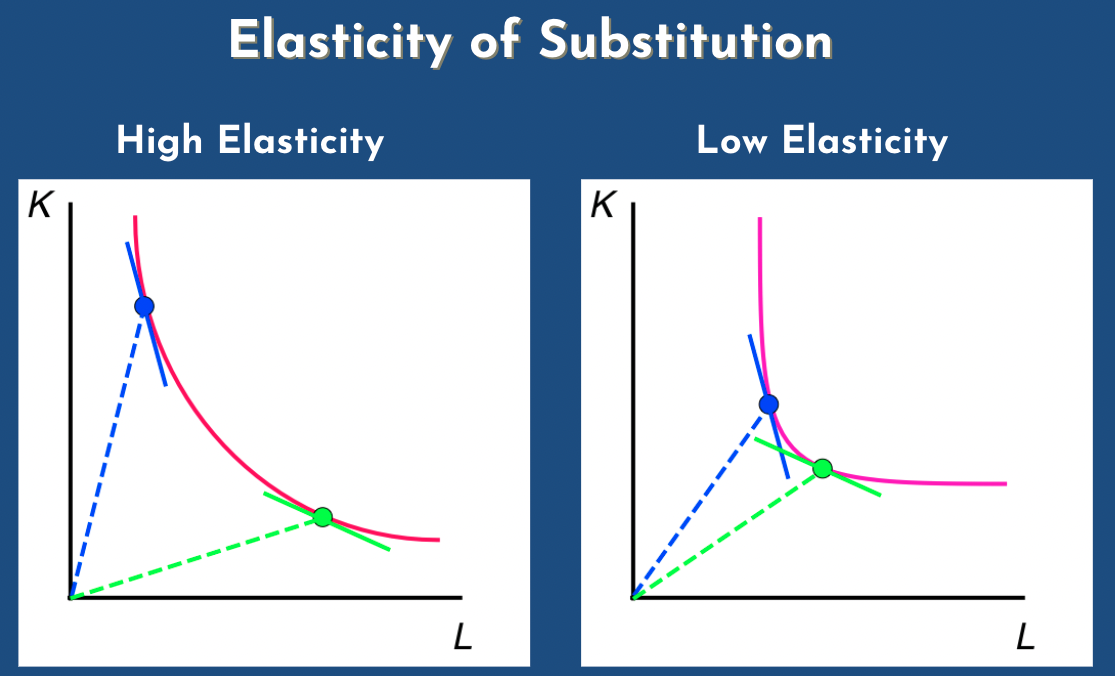
Phil: so a key thing to keep an eye on, is the "elasticity of substitution" between capital and labor in production. And what that is, let's say that the quantity of one of the factors rises by a bit. How much... well, technically it's by how much does the usefulness of a bit more of that thing fall, okay? So, we've got our big factory with two pipes in, one pipe out. Let's say you have one percent more capital going in than you had yesterday but you have the same amount of labor. Let's assume they're complements. They don't have to be gross complements, which is a stronger concept that I mentioned a minute ago. But they're just concepts in the sense that if you have a high capital to labor ratio, a lot of capital per unit of labor, then labor is more useful than if there's a low capital to labor ratio and vice versa.
Michael: yeah, just to to have some clear visual for this. You see in the high elasticity... the upper left point we have high capital and low labor and so if we... this red line or pink lines are isoquant, which is the same amount of output and so here, in this point, if you... as you said... if we increase a little bit of the amount of capital by 0.1, we would increase more, uh sorry, if you oh sorry, if you increase capital then you would decrease a little bit less labor because the derivative is so depending on the derivatives you get how much you'd change need to change the other variables to get the same output.
Phil: that's another way of putting... it's probably a better way of putting it, actually. Well, I don't know. Sure, so if you have one percent, or a tenth of a percent less capital, how much more labor do you need to fill in, and if the two factors are highly elastic then you don't need that much extra labor you can just... you can just sort of fill it in without too much trouble but if there's low elasticity of substitution between them, then if you're running short on capital you need lots and lots and lots of labor to make up for the difference and vice versa, yeah.

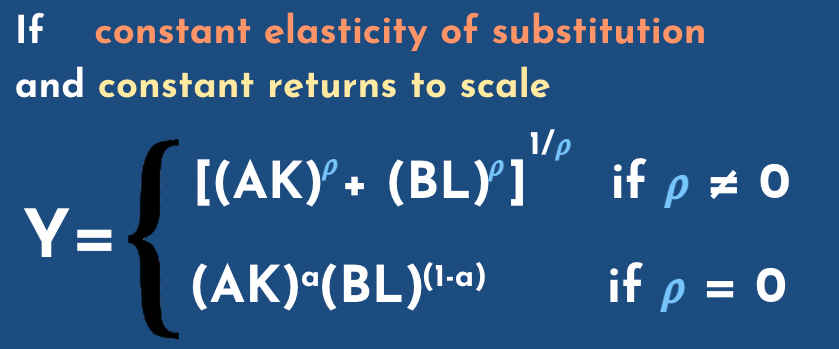
Michael: so I think that this will be more clearer in the next slides where we define... so in your paper you have epsilon, which is elasticity of this substitution and... that's going to go from... I believe zero to plus infinity?
Phil: yep
Michael: and then you can divide... you can do epsilon minus one divided by epsilon and this goes up to one?
Phil: yeah
Michael: and I don't know if you consider case over where it's negative and infinite or something it can go down
Phil: yeah
Michael: so yeah do you have intuitions for this parameter rho, or substitutability parameter?
Phil: I think you don't need intuition for all that much. I think all you really need is to remember the following: if rho is one, that's the same as infinite elasticity of substitution, or perfect substitutability, and in that case it doesn't matter which input you have, it's just: you have humans and robots side by side in the factory or whatever, cutting the hair, and you could just swap out one human for one robot and or vice versa. It's perfectly substitutable, it doesn't have to be one for one, there could be some constant ratio maybe. The robot zips around twice as fast, so a robot's as good as two people, but they don't complement each other. It's not that if you have more robots around it's better to have an extra person or vice versa. So that's rho equals one. As rho goes down to negative infinity you get to the case where they are perfect complements, and that's left shoes and right shoes. If you have more of one than the other then you don't need any more of the one that you have in excess, and again it can be at some ratio, so bicycle frames and bicycle wheels, it's not a two to one ratio but it's the same idea yeah.
Michael: the basic intuition with shoes is that you need both, so even if you don't have... even if you have two left shoes and zero red shoes, you would still buy a right one because you want... you need both.
Phil: right and the marginal value of another left shoe to you is zero. It's not just low in that case. It's actually zero. Now an interesting thing happens around rho equals zero, in the middle there. If rho is greater than zero, even if it's not one, so the factors aren't perfect substitutes, they're substitutable enough that they are what's called gross substitutes. They're not gross complements, which is a term I raised before. And what that means is that if you just have a fixed amount of one of the two things, labor, say fixed amount of labor, but you pile up the capital, then output goes to infinity. You don't need labor and, likewise, this labor goes to infinity, but capital stays constant, output can go to infinity. If rho is less than zero, then you need both. And you might think of workers at their desks. You might be a bit more productive as your desk gets bigger. And as your computer screen gets bigger, and all of that, but as that goes to infinity, as the screen gets bigger, the desk gets bigger, your output just goes to an upper bound and it might not be that much higher than the upper bound you have now. At least I find if I had a lot more capital to help me out I don't know what I would even do with it after a while, maybe 10% more productive or something, yeah.
Michael: I think those examples where rho equals one and minus one are very good to keep in mind.
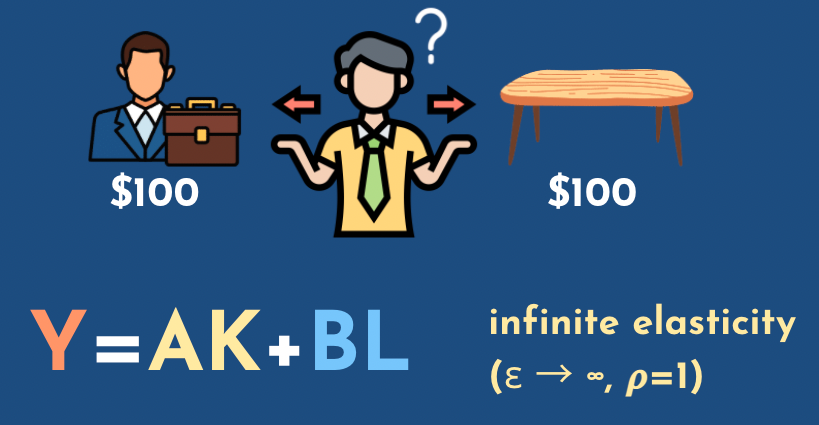
Michael: So with one, as you said, we get a perfect substitute, where you get this formula, pretty simple, where you have the sum of the two, and you could either go for capital or for labor, and as you said, it corresponds to infinite elasticity. So you could just be completely indifferent between the two, capital and humans. I put this diagram with human and desk, because you would only be indifferent between those two if they had exactly the same prices.
Phil: If they were perfect substitutes, yeah.
Michael: yeah, if the price of human labor is too high, you would just go for desk, and the example was minus one... if this example is... choose where you have this fraction.
Phil: no that would be negative infinity
Michael: oh sorry,um, hmm so oh yeah oh that's a mistake because when epsilon tends to zero you go to minus infinity.
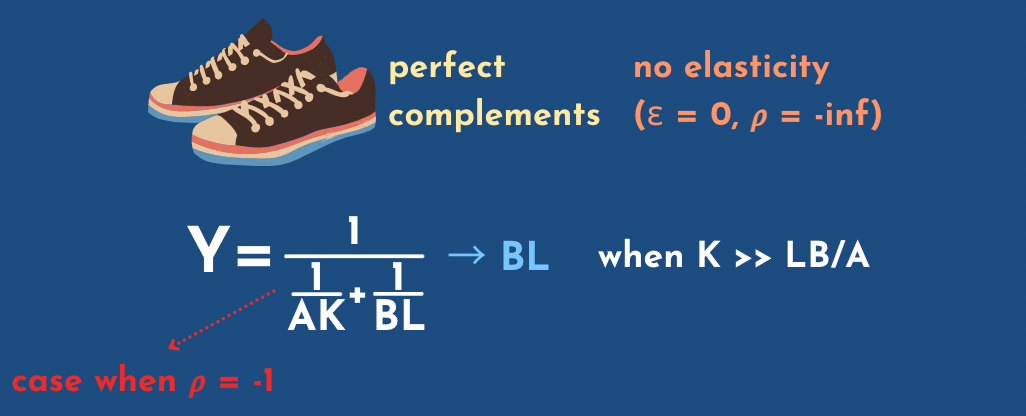
Phil: yeah so there's nothing special about the case of rho equals minus one it seems. There should be, maybe, but I like using it as an illustration of the math because it's kind of easier to wrap your head around than... that funny thing you had a few slides back.
Michael: We have... yeah... so it's not perfect, there's a mistake. This is the case where just rho equals minus one, and you get this simple example where you see when you increase capital too much then you only get it, just the fraction tends to zero and the only thing that counts is labor.
Phil: that's right I think so this is this basic tendency where as one of the factors goes to infinity output just goes to being equal to how much you have of the other factor or linear in how much you have in the other factor. That tendency holds for any value of rho that's negative.
Michael: So I think that's interesting to keep in mind. This example of simple math for when rho is negative... or when rho is always positive. We have this sum and and then
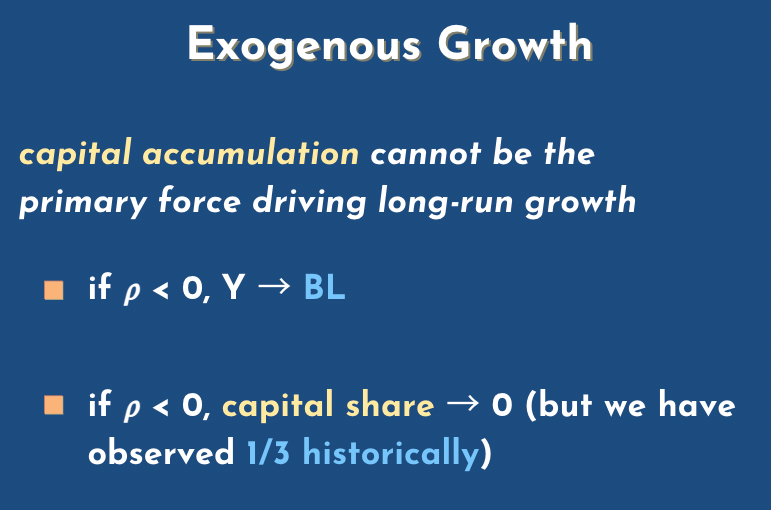
Michael: there's this concept of endogenous versus exogenous growth. I think one line of your paper is "capital accumulation cannot be the primary force driving economic growth", and then you go into different cases for why it's not the case. Can you delve into that?
Phil: Sure, so empirically it seems that, at the moment, before we've come up with... AGI... capital and labor are gross complements. So rho is negative, and what that means is that you couldn't sustain growth just by piling up the capital, because it's like people sitting at a desk and the desk gets ever bigger and you have ever more pens in the drawer and, like, what do you do with them? So as as we piled up the capital we would just get output going to an upper bound and that would be proportional to the number of people. So that's why Y goes to BL, thing you have. And another thing that would happen is that the capital share would fall to zero because it would be like, well, this gets, this is why the elasticity of substitution point is sort of relevant... the thought is: as the number of desks grows, and grows by one percent, then another percent, then another percent, what happens to the marginal product of an inch of desk space? It falls. But how fast does it fall? Well, if rho is less than zero, that is if the elasticity is less than one, the marginal product falls by more than a percent every time. So you have one percent more desks but the rent that they take... that each each desk lender gets, follows by more than a percent.
Michael: okay.
Phil: and so that means that the amount they're all getting collectively is shrinking even as the amount of deaths is rising and they stop investing at that point... or they probably stopped investing but if they didn't, just theoretically, if they for some reason just kept on building desks and letting them out at evergreen, then the capital share would go to zero right, because for every percent extra desks you have, you have less than now, percentage falls by more than a percent okay
Michael: and probably people would also like would you increase of... that they would also have to have more human labor and so this human labor would represent more of this this share of output.
Phil: That's another thing happening. It wouldn't matter after a while, but at least for a while human labor would be getting more productive and that would raise the wages.
Michael: So that's why, like, just investing more capital couldn't sustain growth
Phil: couldn't sustain growth in the long term, and it would lead to a capital share falling to zero but historically we've observed constant capital share and we have seen growth, so capital accumulation can't be what's going on.
Michael: There's some contradiction with empirical facts.
Phil: Not in isolation.
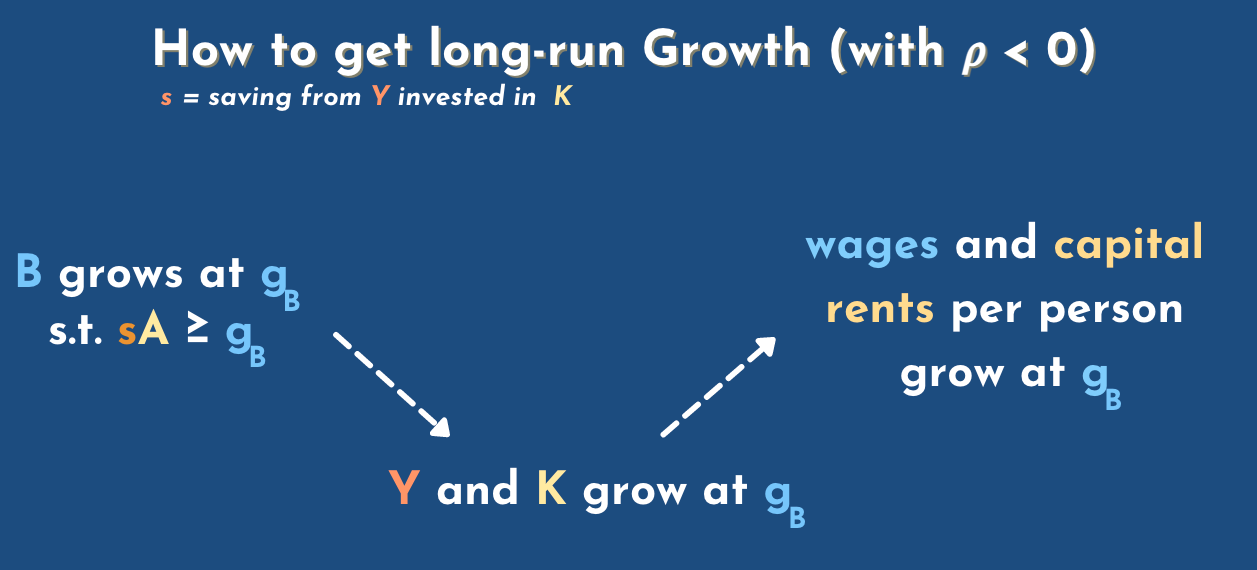
Michael: And then there's yes when we consider negative rho so elasticity less than one this is in your scenario where conditions... can you explain a little bit those scenario, and how to get long run growth?
Phil: sure. The way to get long run growth in output per capita when rho is negative, that is when labor and capital are gross complements, is to have labor augmenting technology. That's the only way to do it. The reason is, that to get growth in output, not per capita but just output period, you need growth in two things. First is either capital or capital augmenting technology. You need more of the second thing. What you need is more BL. You need more effective labor, but so when it comes to growing the stock of effective capital it doesn't matter whether that comes in the form of more actual capital or more capital augmenting technology: either one is fine. But when it comes to growing the pool of effective labor, that can't come from just growing the number of people because then you just have more mouths to feed. If you want more output per person you need growth in B, that is labor augmenting technology. And so that's the first step: you need be growing at some rate and...
Michael: I thought one thing important... we did talk a lot about product output and GDP, but we never talked about the distinction between people consuming this GDP and or people investing more so maybe you could explain that as well?
Phil: sure, so we talked about all the final goods that came out the pipe at the end of the factory. That's GDP, and I think I might have sloppily said we're just talking about the consumption goods, but I shouldn't have said that, I'm sorry. I should have said "the final goods", and sometimes it's not clear what counts as a final good. It's true, like with the eggs in the cake, right? Is the cake the final good or is the egg the final good that you bring home and use to bake cake. Well in the same way it's a little unclear what's the final good when what you're making is a widget that's then used next year in a factory to make more goods. But anyway let's put that aside and say okay we're just looking at all the final goods produced this year: that's GDP. That includes haircuts and cars but it also includes light bulbs which are not used at home, but are used in a factory to light the place up and let workers work on cars for next year. So that's GDP. Now, remember, we need two things growing to get growth in output per capita. We need growth in B and we need growth in AK. Now let's say A is fixed, so there's no capital augmenting technology growth. How is K going to grow? Well that's what's called saving. That's not consuming all of the output of the factory. Not consuming all of GDP, but using some of it to make more stuff next year, or whatever in the future, so using the light bulbs to light up the factory and not the home...
Michael: or you could just sell sell your stuff? Sell what you produce and then buy more things with the money you make from selling?
Phil: well yeah, but let's not think about... we're thinking about the economy as a whole. If it's the whole world then there's no one to buy or to sell, so... if the savings rate is high enough, then growth in K will be enough to keep up with that growth in B, that g_b, so if B is growing at two percent a year and the savings rate is high enough then you'll have both those inputs to the big factory of the economy, the metaphorical factor growing at two percent a year, and output will also be growing two percent a year. If the savings rate isn't high enough then we'll be constrained by capital eventually and output will be slower.
Michael: right, and at this point you show that output capital growth at the same rate as the labor, superior to g_b, and you get as well wages and capital rents per person growing, so that would sustain long-term long-run growth.

Michael: You made the distinction between endogenous growth and exogenous growth... so could you maybe explain the distinction?
Phil: sure, so as noted we need growth in B, in labor augmenting technology, to get growth and output per capita. We've observed and hope to keep getting... does that growth come from, well, if you're not really going to model it, but you're just going to say, well, somehow B grows at two percent a year and we'll think about the rest of the economy, assuming that's what happens: that's called exogenous growth. But if we're going to actually model where that growth in B comes from we call it endogenous growth. And there's a certain class of models that I think is most plausible, sometimes called semi-endogenous growth models, where growth comes not only from scientific research and applied R&D, but more kind of further down the pipeline, but it comes from people working. But you need growth in the number of scientists to maintain growth and output. You can't just have a constant number of scientists leading to exponential growth and output: you need growth from the scientists and where do growth and sciences come from? Population growth and growth in education—we're not going to model that, we're just going to say that comes out of the sky. So that's why it's called semi-endogenous, but it's it's more endogenous than exogenous, you're at least kind of explaining...
Michael: so endogenous is "comes from inside" whereas exogenous is "from outside"?
Phil: basically, yeah
Michael: and without going too much into the math, but if you have this growth in B that comes from scientists... scientists are a fraction of the labor force that work on, maybe more labor augmenting technology, and from this paper we mentioned, "Are ideas getting harder to find?" we can see that sometime scientists can collaborate and do great stuff and be complementary, or they can step on toes and you need to invest more in research to get more done. So is that the intuition between the parameter lambda, or?
Phil: in this model, lambda ends up not mattering much for the model but, yeah, lambda equals to one would mean that if you double the number of scientists at a given moment, you double the rate at which they come up with increases to B. Increases in labor augmented technology, and if lambda is greater than one then the relationship between number of scientists at a given time and advances in B is more than likely doubling the number of scientists. It leads to more than a doubling in the speed at which they crank out the increases to labor augmented technology, and if land is less than one it's the other way doubling the number of scientists... less than doubles the contributions in... intuitively we would think that lambda is inferior to one. We have diminishing returns in having more scientists or having more labor in science. I think that is what we tend to observe though. I don't know if that's because of duplicated work or just because you're going to choose the best if you're only going to have a few scientists it'll be the if there's only a little bit of research funding it'll be the best ones and then as you dip ever deeper into the dregs you might double the number of scientists but you won't double the number of IQ points.
Michael: and I guess the other kind of parameter for this model is kind of this power to this labor augmenting technology, this parameter phi... where depending on where it is you can either have something that stops the growth in labor augmenting technology, or leads to type I or II singularities. I have a hard time kind of understanding this parameter. What's the intuition behind it? And you have mentioned that it is empirically at minus 2.1, or at least that's one estimate. Do you agree with that estimate? If you remember... if you remember it? Or can you explain what's the number?
Phil: I'll explain what it signifies, and then comment on it. I call it the research feedback parameter. If it's equal to one then we have purely endogenous growth in the sense that we don't need any increase to the number of, let's call them scientists, to maintain constant exponential growth in B, labor augmenting technology. So that's positive research feedback. What's going on is, sorry I should have explained this first: if phi is positive we have positive research feedback meaning that the inventions we've already come up with, will help us in developing further advances in labor augmenting technology. So we have computers, and those help us in our projects to develop the next big thing after computing. If phi is negative then that might still be true. Inventions in the past help us with further technological advancement but there's this other factor which outweighs it, and it's the fishing out effect: it's that given that when we've already invented something as great as a computer it's harder to invent the next thing, because the next thing is even more complicated and that wins out even though we have computers. We move more slowly with the same number of scientists because things have gotten so much harder and so... if phi is negative with a constant number of scientists, things just get harder and harder and, the level of technology rises to an upper bound then it gets stuck. What you need to maintain growth with phi being negative, is you need to sustain growth in the number of scientists. And, as you mentioned, there's a paper from... well it's a few years in the making but just published last year, "Are ideas getting harder to find" which tries to estimate phi and finds that phi is quite negative.
Michael: You need to invest much more money or people, more labor, to get these new advances in Moore's law or other scientific adventures.
Phil: yeah, the key issue is that you need more people, if you just needed more capital then more money just bought capital equipment then actually you could sustain growth and output per person, even without the scientists multiplying because you could just pile up the factories to do the science and the real issue is that you need growth, and growth in labor input, but we're trying to get growth and output per capita.
Michael: so I think now at this point, we kind of have an idea of this parameter phi, this research feedback. Maybe we can go over... more generally the different kind of scenarios you draw down the line.
Phil: you asked me what I thought of the estimate for my argument
Michael: oh sorry
Phil: what they do is they sort of look at a bunch of different industries and estimate phi in those industries, but actually it varies a lot across industries, and it's just for the economy as a whole that it seems it's negative. If I remember right, the only industry in which it's positive is actually in Moore's law. I've forgotten about this when... oh no, maybe there's two, but anyway. One of them is in Moore's law, so it seems that the better computers we have aht the faster chips help us make faster chips, buy more, then it gets harder to make faster chips because we would pick the low hanging fruit and that seems very significant especially when we're trying to make projections because if a kind of growing fraction of the economy is being done by computers, or whatever, then maybe the positive feedback loop part of it will end up taking over, and so it's sort of a mistake to think that the composition will be the same and so you have this average negative two. That's constant in the future.
Michael: so if for AI and Moore's law, it's positive, and for other scientific endeavors it's negative, and in average negative, it doesn't mean that we couldn't get labor, and we need to have it as a bigger term because most of it would come from AI or something.
Phil: exactly, and this is something I haven't really paid attention to when I talked about this on "here this idea", or I haven't really thought about too much until recently, but it's only slightly positive and it's zero... it is very much in the error bars. So I think more research on actually confirming that there is this area of positive research feedback would be valuable and picking it apart right, because it might be that it's negative in the domain of AI even though it's positive in the domain of just fitting more transistors on a chip and so that's all I have to say about that.

Michael: Cool. I think we can just skip the the next one and just go on the different scenarios. So the HS means high substitutability, PS perfect one, so these are the different values for rho, our substitutability parameter, and then I think... plus is when it increases in a significant way, so the type I, not a significant increase but... the labor share could go to a constant C, or to zero. And I is a singularity of type I. So... what's the intuition between those kind of three scenarios?
Phil: okay well we skipped over the first scenario where we talked about different kinds of consumption goods. That was on the previous slide, which we skipped, and I think it is maybe a bit of a digression so I won't say anything about the first line. In the second line we're dealing with a model in which you have that factory of the economy with the two pipes in and the one pipe out, but now, instead of rho being negative as it is now, and has been positive, it could be between zero and one, or it could be one, but either way here's what's going to happen: the growth rate is going to accelerate. It's going to rise because now growth isn't bottlenecked by growth in B anymore. Once rho is positive, you don't need growth in AK and growth in BL, you just need growth in one of the two. It could be either one. And, in particular, it could just be growth in K, so if you just have a high enough savings rate then it'll... then you could have a growth rate just, you know, if A equals one, which actually seems about reasonable right now, then let's say we save 12% of our output every year then what's the growth rate going to be? It's just going to be 12% in the long run.
Michael: because we're just saving all that and invest that in capital.
Phil: yep, so this is 12% more every year... what happens to the human labor share, or the labor share: it goes to zero because the number of effective humans is staying the same but you have this capital that can
Michael: massive pile of capital
Phil: massive pile of capital that is substitutable for the labor, so it's just more and more robots, same number of people. So the fraction of payment going to the people is just going to zero. What happens to wages? Well in this case actually it depends on whether labor and capital are perfectly substitutable, or just highly substitutable. If they're perfectly substitutable, then wages should just stay the same. So wage growth should just stop if there's no labor augmenting technology, and if there is labor augmenting technology, well the wages keep on rising at the rate of labor augmented technology growth because you have the robots and workers side by side and they're very substitutable... or if they're perfectly substitutable. And so the explosion in the number of robots doesn't affect the productivity of the people beside them so their productivity stays the same. Wage stays the same, unless they get more productive, in which case the wage rises if they are... if a labor in capital... only become highly substitutable though... then because you have this explosion in the growth rate because saving is enough for growth... so the growth rate rises to 12 percent or 20 or whatever, you also have an explosion in the number of robots or the amount of capital that's substituting for labor. However it's doing it, and with rho less than one, even if it's still positive, because we're insisting on its high substitutability but with rho less than one having more of that capital around raises the marginal productivity of labor, does that make sense? So you have you have wages rising and the wage growth rate rises
Michael: so it's a distinction between perfect substitutionability and still suitability but not perfect, and depending on that parameter you would have either the human wages so... we're talking about the second line right?
Phil: yeah
Michael: yeah but if it's not perfect then you would you would have the wages growing.
Phil: yeah
Michael: tthe most interesting kind of scenario is the third line where you have both wages and growth on a type I singularity. So for me it's kind of hard to understand why... how a human would behave with an exponential growth... an exponential wage, what would they buy? What would they do in this scenario?
Phil: it would have to be super exponential—we already have exponentially growing wages.
Michael: right, it's super exponential, so that if the growth rate grows exponentially
Phil: yeah, it is hard to imagine though I think it would have been hard to imagine in the past. Like someone in medieval times might have said "what would we do with with a million dollars to spend every year or something on ourselves. But we can have a big castle, but then what a bigger castle?". As time goes on, as people get richer, new products are developed that means it gets back to something we were talking about before: new products get developed which are, you know, people enjoy buying or spending their money on. I don't know what the products of the future will be but I wouldn't push past people to come up with ways to waste a lot of money and spend a lot of money.
Michael: I think it's interesting to just skip. I think we got the intuition for kind of this imperfect substitute scenario. I think it's interesting to go over...
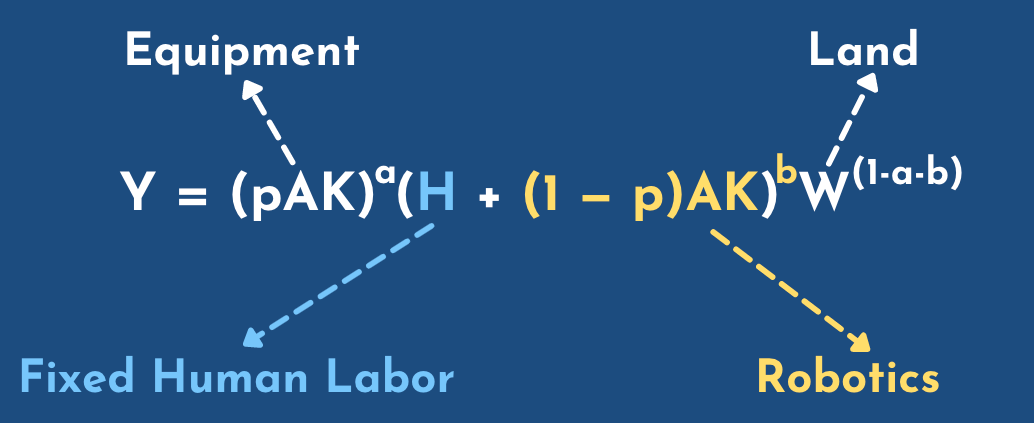
Michael: if you talk about your medieval guy, at some point the parameter of land was very important so I think in this model... I think it's adapted from Hanson, a paper from Robin Hanson, and you have this parameter of land, and you also have robotics and a fixed amount of humans... so I find this very interesting. Could you maybe explain a bit?
Phil: sure. So in the third line from the previous slide we got a type I singularity because we had capital augmenting technology growing exponentially, and at the same time capital was growing exponentially, so you have this exponential thing growing exponentially, and capital... enough capital, alone is enough for growth. Here, we're looking at a different model in which human labor and capital are perfectly substitutable... in which you can have capital augmenting technology growing, and you can have capital growing, but you don't have a singularity. You just have a boost to the growth rate. And the thing that's different about this model is that now labor and capital aren't the only two factors of production: you have a third thing which you sort of need as well, and that's land. The amount of land is fixed and...
Michael: is the fixed amount of land an important consideration? Do you think it is a reasonable assumption for like, we're doomed to stay on this planet and we cannot build gigantic buildings, so we have this fixed land? Do you think it can be relaxed? And you can think about making buildings with more land in the building? Or colonizing new planets or something?
Phil: I don't know whether we'll ever ever be able to colonize space. It seems very hard. But at the same time we just went over the course of a century from horses and buggies to putting people on the moon. But to maintain exponential, sorry to maintain the singularity you would need exponential growth... in... actually I don't know if that's true. What do you need exponential growth in? Land maybe?
Michael: Hanson maybe thought about this?
Phil: Well, no, this isn't Hanson's model actually. I sort of adapted it from Hanson's paper but Hanson just sort of got rid of the singularity by making output less then... decreasing returns to scale, in labor and capital, whereas, before we didn't talk about this but the other models assumed constant returns to scale and labor and capital... so the idea there is if you just double the number of factories and the number of workers working at them, what happens to output? Well, it just doubles, right? That kind of makes sense. But no! Because we forgot about the land. If we just had twice as many factories and twice as many people, but the same amount of land, then you have to start putting the factories on land. That wasn't so suitable for a factory, and output wouldn't double. It would rise by a bit less, and that becomes more and more of a problem as the ratio between the amount of land and the amount of other stuff, capital and labor, as that falls. But anyway, so Hanson just made output decreasing returns in labor and capital. He didn't specify land. So he just had pAK to the a, times that other thing to the b, where a plus b is less than one, and I just spelled that out a bit more by introducing land and having them add up to one again, having the exponents add up to one which is more conventional.
Michael: I think it makes sense for me.
Phil: But I was going to say, if we colonized space, then even in the best case scenario land would only grow cubically, because it'd be a sphere of the earth going outward
Michael: and we need exponentially
Phil: so I don't think that would be enough for a a singularity in practice but, anyway, again, that would be kind of probably pushing the model beyond.
Michael: I guess if you if you really want to push it, you could say that... if you want to test it, what you need is not land... it is kind of resources and energy at the bottleneck of most physical processes, and to get energy you could do a Dyson sphere or something on the sun, and maybe the next centuries or thousands of years you would have even subtler ways of using energy and improving the rate of creating energy.
Phil: so there is that limit of just perfect efficiency.
Michael: so here I think what I understand of this model is... when instead of considering labor augmented technology we have this fixed human labor, and then we can just spend our capital to buy more labor directly, so that's the fraction one minus p that we spend on capital, that can be used into labor and so that that's a perfect substitution. That what we see is an addition between the two and so we can just spend a lot of capital to get more growth and then we just invest more in capital, is that the basic intuition?
Phil: yeah that's right so again in this model labor and capital together are not enough for growth. there are enough... okay so it's sort of right on the edge. I mentioned what happens if rho is positive. What happens if rho is negative in this case? Rho is zero exactly, and what that ends up meaning is that whereas you would otherwise have a type I singularity, with capital augmenting technology growth, and perfect substitutability between labor and capital, here you just get a growth rate increase. Iit's sort of a funny little edge case but when rho equals zero then it sort of bumps down a singularity to a growth rate increase.
Michael: Okay, still interesting, I think it's an interesting equation to think about. So yeah I think the one we get after is the different scenarios. I'm not sure if it's from this equation. I guess, we get those different scenarios. I'm not sure how much we should delve into all of them or if there's one that is especially interesting to you.

Phil: I don't know. We were just talking about the one on the second line. I guess earlier we were effectively talking about the previous line. We talked about the perfect substitutability in production. There's no land constraint, and you have capital augmenting tech growth, but you get human wages stagnate, and you get that type I singularity.
Michael: If we have no land, then we have type 1 singularity growth, and wages are infinite.
Phil: If we have no land constraints. Quickly the difference here is that instead of having capital augmenting technology growth on the whole we only have technology growth in the the capital that complements labor so we only have ways to use metal more efficiently in the machines that the robots use in the factory... the robots or the humans, but when it comes to the robots we can pile up the robots but we don't get more efficient at making them and they don't get more productive. In that scenario human wages don't fall to zero, because you have kind of two things balancing each other out. One is that we can make more and more robots, which are competing with workers, but on the other hand we have more and more equipment for these robots, and workers to use, which raises workers' wages. But the robots lower the workers wages, but the equipment that gets more efficient raises them, and those cancel out, and the wages just stagnate.
Michael: So I think that's an important distinction. How do you distinguish equipment from robotics? Robotics can help for human labor whereas equipment is just to help humans?
Phil: Robots do labor, and equipment complements labor.

Michael: Interesting. You're talking about what would happen if robots could do the work to get more robust. So you're pointing at somehow the self-improving robots in this model.
Phil: They're not self-improving in this case, they're just self-replicating. In the model you have on the slide and I think the main contribution of this model... this is the Mookherjee and Ray model, is to point out that all the other models we've talked about so far let robots build everything. So they're substituting for labor, whatever we're trying to make, but the important thing is sort of not whether they can do everything but whether they can make other robots. Because, no, the way I should put it is: even if they can do everything else, as long as humans remain necessary in making robots, then humans will still maintain a positive labor share. And so we can we can think about the implications of substitutability in robotics production in isolation instead of in the economy as a whole. I don't think this adds all that much to be honest but it's worth...
Michael: what doesn't add all that much in these equations?
Phil: I guess it just... the question is "how can people maintain a positive labor share?", if that's your question? "How can people remain necessary for production?" Well, what matters is people being necessary for the production of something that is necessary, or something that people want, and won't just use robots to do instead. And that can be through... a lot of people have noticed that there are a lot of jobs that we prefer done by humans, so some artisanal bread or artwork, or care home work. There might just be some kinds of things we want humans to do, and if we wanted enough we might use our newfound wealth with all the growth that AI brings to just hire lots and lots of people to give us massages and serve us their homes and make us artisanal bread and everyone might end up doing that and you have a positive labor share or growing wages, or whatever it is that you're keeping an eye on. Whatever variable... and one of the ways that people could remain necessary is by making robots... if people are necessary for the creation of robots, but I don't think that's all that interesting. It's just a specific case of a more general observation that we already knew about.
Michael: so you're saying, essentially, that if you want to keep humans, having good wages and having a substantial fraction of the labor share, we should have humans doing something useful and then they could be paid by this amount of growth we have, we could give it back to the humans doing something useful and humans doing robotics is a special case of this.
Phil: If humans are necessary for doing robotics, and they're at least as useful as robots or complementary I think.
Michael: so I guess if this model is not very interesting, for me, one thing that's has happened in the past in... I think this year, was this company OpenAI releasing something that enables humans to generate code with their model. So you can just start coding and it will auto complete your code with their model directly, and I've used it a lot, and every time I use it, it generates useful code that I can read and reuse myself, and if you think about the system "developers using this, even OpenAI developers, employees plus the model", when we write more code using their model, we can then use this code to improve this robot, or this AI software, and so we're getting in a sort of closed loop where humans are kind of useful but they're not the only part... useful for making code, now AI is also accelerating this.
Phil: yeah but that was already true before, right? We had capital helping out, with the process of improving AI. What will really be the qualitative shift, will be when you don't need the human in the loop. When it can just work on itself without any human
Michael: and if you make the... if you make the human faster. If you make the human writing software, or AI code faster by helping him write more code with AI, would it affect? Do you think, intuitively, it will like lead to faster growth and a type I singularity or, and your view doesn't really change that much in your models?
Phil: again you keep calling them mine: they're not mine.
Michael: oh sorry, in the literature reviews
Phil: I'm not claiming any credit. Okay, so that is an interesting thought, that would be different from what I said. So what I said was that, would it just be capital, that's we already have capital complementing people doing stuff, but this would be a case in which capital is not substituting for labor but making labor augmenting technology grow. So the humans are getting more productive. One programmer can do what it used to take two programmers to do, and I think the model.
Michael: I think this could go into labor augmenting technology. If you're coding faster you effectively maybe...
Michael: I think the the next ones are are essentially different scenarios. I don't know how much we want to go into these ten different scenarios or something, what do you think?

Phil: I don't know. So these these two lines right here are about the thing we just talked about right now, about substitutability in robotics production. In particular... I don't have much more to say about them than I already said, but for later slides, I don't know.
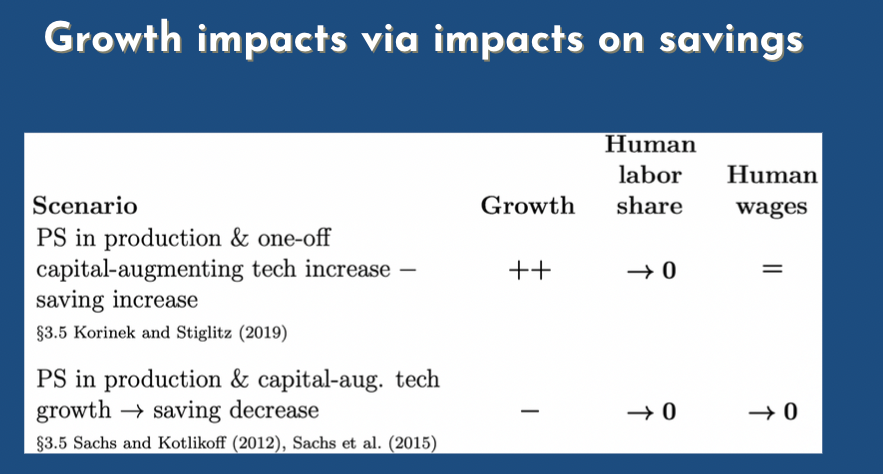
Michael: Then there's the the impacts on savings, oh sorry, how savings can have an impact on growth as well
Phil: so this is also a little bit tangential but maybe worth noting briefly. So in a world where capital can substitute for labor well enough, so if rho is greater than zero, the savings rate can affect the growth rate. Remember before for labor and capital, where gross complements... where rho is negative basically, what drove growth in output per capita, was growth in B. And if the saving rate is too low, then growth is bottlenecked, but as long as the saving rate is enough to keep up with growth in B, then further saving doesn't increase the growth rate. But, once rho is greater than zero, then you can just pile up capital and get more and more output. So increasing the savings rate does increase the growth rate, and it could be that something about AI causes people to save more, or save less than they were saving before. And there's a lot of stories you could tell as to how that would happen. And there are two of them that people have written papers about, but in principle you can imagine a thousand ways that AI would affect the savings rate and it would then affect the growth rate, if rho is greater than zero and...
Michael: when we mean saving, it's not people literally putting money on their bank account or... it's more people investing in S&P 500 or companies right?
Phil: that's right. It has to be am investment. People use the term saving rate, but more accurately would be investment. To say it would be invested with...

Michael: and then there's this whole, I think, this whole literature review part on task-based models for good productions. Could you explain briefly what that is?
Phil: Sure, so as we mentioned a while back, the growth increase... the growth rate increase that we've been benefiting from since the industrial revolution I think, can be pretty well thought of as capital doing ever more tasks that labor used to have to do. So the steam engine or whatever, we now can make machines that do things that people used to do, and at first glance that sounds a very different model of what's been going on with growth, than the model we were talking about before, in which you have labor augmenting technology and capital augmenting technology, and, there's no tasks in that model. You just have the factory with two pipes in one pipe out, and remember capital augmenting technology was meant... you could use less steel for the cars, maybe labor augmenting technologies, one person figures out a technique to operate two machines at once, but where's the substitute? Where's the task replacement? It's not clear. But, it turns out, a paper from just two years ago shows, that the two are basically equivalent. So if rho is negative (if capital and labor are gross complements) then you can basically... if you imagine that what's going on inside the factory is a whole sequence of tasks, some of which you can use labor, sorry, some of which you can use capital for, and the rest of which you have to use labor for, then as tasks get automated, that ends up functioning like labor augmenting technology. And the way it works is I think pretty interesting. So let's say we start out with 40% of the tasks being done by capital, and the other 60% being done by labor. Because you've only automated the first 40% so far. Then, on average each person sort of has to spread their work across six... this is a hundred tasks... they spread it across sixty tasks
Michael: because they're not automated.
Phil: they're not automated right, and so for every person you add into the person pipe of the big factory of the economy, output only increases by a little bit, because that person has to spread their work across a lot of tasks. In practice they would specialize, but on average you understand each person in effect is spreading their labor across a lot of tasks and you just have a little bit of capital on the side doing the other 40% tasks, and output only goes up a little. But then let's say you automate half of those 60 tasks, so now only 30 tasks are done by labor. Now each person in effect does it... can be responsible for twice as much output as before, because they only need to spread their work across half as many tasks. Capital takes care of the rest, so it's sort of doubling B. You see that?
Michael: I get the intuition.
Phil: and you can have this exponential growth in B, that we've observed, just by having this constant fall in the number of remaining non-automated tasks. So that goes to zero. The number of tasks you need labor for goes to zero asymptotically, but you never quite get there. You always need people for some little bit at the end. And that ends up kind of being the same as growth in B. So anyway, you have all these task-based models of AI, as they're called. And if you just introduce a task-based model to a model with growth in B, separately. So you have automation, and people getting more productive at each task, then that increases the growth rate, and it shouldn't change anything about the labor share. So what does that mean for wages? Well, if the growth rate rises, and the fraction going to labor stays the same, then wages have to rise. So those are those two scenarios in the middle there. But if you kind of automate everything, if you automate all the tasks, or if you kind of shake things up more deeply, then you can get a singularity, rather than just more growth
Michael: and that's when growth and wages grows super exponentially, and we have seen a singularity of type I. I think I got... I think it's interesting that we can make a parallel with task based models and the other ones.

Michael: I haven't even looked too much into AI in technology production.
Phil: well, I think this is kind of the most interesting part of it.
Michael: Okay so go for it.
Phil: we get to self-improving technology. As we can see there are a lot of different models here, but here's where we're finally seeing some infinite output in finite time. And what's going on there is, remember, these semi-endogenous models from before where, you need growth in the number of scientists to maintain output. Well, if you have robot scientists, then basically you can get this feedback loop where you have super exponential growth in scientists, leading to super exponential growth in technology. But if the technology is capital augmenting, and the scientists are made of capital, that means effectively you have more scientists next year. And that's the real crazy feedback loop that could lead to an AI singularity.
Michael: And I believe people like to talk about scientists as something very abstract that is hard to automate because the scientist walks into a bar, has a wife, and does a bunch of human things, but if you just replace science in AI with people coding things, and slapping their fingers at computers, and getting more feedback from what they do... I feel those those robot scientists could just be AI generating code... AI generating AI code is already for me a robot scientist in some sense.
Phil: sure. We need more than computers at the moment to actually develop products and stuff, and have a better understanding of the world so... I think you're frozen
Michael: oh sorry
Phil: no you're there.
Michael: Yeah so it depends on on exactly where what we're focusing on. If we're talking about creating products that can be consumed, yes we need humans to do the carrying, the cooking, and all of those things. But if we're talking about production of software, the AI can... the AI and the human are in a loop where the AI now can suggest code for the human to read and the human then understands it and accept or not. The code degenerated and... I don't see much more than this, two things human accepting or not accepting and the AI suggesting more code.
Phil: But that's if we're just making code.
Michael: But you don't need much more than code to create an AI, it needs the servers and electronics and net networking behind it.
Phil: sure but that's all for AI getting better and better at being AI. What I'm saying is one thing that you need to have an explosion in scientists more broadly speaking is you need systems, I keep calling them robots but whatever, you need systems that can do all of the things we call AI R&D, not only some of AI R&D. We need... oh we ultimately need a system that can replace human contributions to developing new kinds of computer ships and... whatever
Michael: I think the control argument to that is as what we're actually interested is having AI that can automate human intelligence, and so as long as we have something as general as a human and can think and communicate with humans, and strategize, and those things, then I believe that if we only have code that that self-replicates and becomes better at coding until it reaches just human level intelligence, at this point you can just ask humans to do stuff for him, or manipulate humans to do stuff for him, and so you don't really need more food or human science because now the AI can do whatever he wants by just sending requests or orders to other parts of the world.
Phil: But if there's only so many people, and if people actually remain necessary, then
Michael: oh it wouldn't be enough... it wouldn't be enough to sustain an exponential growth. I got you.
Phil: I think it's worth remembering that intelligence isn't the only input to at least... unless you define intelligence more broadly than where we naturally do intelligence is the only input to R&D... when coming up with new products for instance. Having an intimate understanding of human preferences strikes me as an important, an important factor that machines probably won't have for a long time, or maybe a short time, but it'll be one of the later things for it to beat us up. You might have a friend who's very smart, smarter than you, but doesn't know your preferences as well as you do, and likewise I think we could have an AI that's sort of more intelligent than any human being in every sort of every dimension we call intelligence, but doesn't really have quite as sophisticated... an intuitive understanding of what product will really tickle our fancy, and you would need that to kind of sell this product to humans... just to think of the product in the first place. Okay, oh this is going to be a really good one, oh that's not gonna, no one's gonna use that okay, I'm just saying to really replace people for everything you don't... we casually use the term artificial intelligence but we're not just about intelligence, and you would need artificial arms as well, and we're familiar with that problem. The difficulty of building robots with as much dexterity as people have, that's not the same as intelligent and, and just another thing is there's this intimate understanding of human preferences which... intelligence can help you get that, but it's not identical to intelligence so...
Michael: I think there's this definition of intelligence as more closer to what humans call IQ and ability to think in abstract and logical ways, and then there's this more general definition from, I think, used by Bostrom in his book Superintelligence, as the ability to achieve one's goals, where if you don't have robotic arms... if you don't have human arms, and not with as much dexterity, and you're not able to achieve one's goals, then you're considered less smart than someone else. But in a common sense that doesn't count as intelligence.
Phil: I think that's right we didn't think of Stephen Hawking as less intelligent because he was in a wheelchair... if anything that made him seem more intelligent. Also, the ability to achieve your goals, I think that's like, even if a machine had all the things we conventionally call intelligence and had arms and was much better than a person achieving their goals, whether people will use it to replace all their human scientists and developers depends on whether it's better than a human at achieving the robot owner's goals and the robot owner's goals might be to come up with better better potato chips, and the robot might not know
Michael: okay... so I guess it doesn't doesn't really... you can have something that is intelligent or or able to stuff in the abstract but you need to have humans that are actually interested in using the thing, for other humans products or preferences that's interesting
Phil: that's right, I think that's sometimes overlooked and that's not relevant if you're Bostrom and you're writing about Superintelligence, you're not even thinking about a scenario in which people continue to own and fully control what these things do, and just decide to use them for this and not for that, we're thinking about the danger that comes with the robot that can have scary goals, and execute on them and... for that all you care about is that it's smart and it has arms. You don't care about whether it knows what kind of potato chips people like... but if we're talking about what effect it will have on the growth rate in a scenario where it stays under control, then you have to think about this other thing as well so...

Michael: I think that that's a perfect transition to our the conclusion of of this whole presentation where, I think at the end of your little literature review you mention that, or maybe it's in the "here this idea" podcast, that economists don't really consider long-term growth increases, and they mostly consider that it will maybe increase by a few percent, but they don't consider dramatic increases, lead apart singularities or something. So, yeah, do you get the impression that there's more and more paper about that, and economists are starting to consider those scenarios? Or are you the only one that... okay not only one because you've done a literature review, but are there more papers being written about this?
Phil: I don't think so. I kind of hoped so. When I wrote this thing I saw a number of papers that considered these singularitarian scenarios but... I was actually at a little online conference... not a pretty big, but online conference on the econ of AI last week hosted by the NBER, National Bureau of Economic Research, and, Anton Kornick, the co-author for the literature review, did a survey of all of us there, on questions about like, "what we thought would happen to the growth rate given AGI" and so on, and only a small number of people thought there was any more than a one percent chance, let alone a 10% chance that AGI would lead to any kind of singularity, and people's projections about the growth rate over the next century (or I think next century was what we were asked about) were very boring. People thought it was almost certainly going to stay around two percent a year.
Michael: what was the population what were there singularitarians or did you have more traditional economists?
Phil: it was entirely traditional economists.
Michael: and what do you think? Are you part of the one percent? Or do you have a more nuanced opinion?
Phil: No, yeah, I think conditional on AGI, the chance of a singularity is more than 10%. I don't think it's like... I don't think it's guaranteed. I forget what number I put down but I've sort of wavered on this, but maybe I think there's a one in four chance of it or something.
Michael: Okay it's 25 percent, yeah it's a bit hand-wavy. We don't have any quantitative estimates on that. I guess it's more kind of more a gut feeling. One thing that makes me laugh at your conclusion in your literature review is that you mentioned that, as long as humans are still a little bit useful for work, they could just stop working and go on strike and then receive a lot of human labor, oh sorry a lot of capital... or wages, and we could have, yeah, things where you can just invest more capital and get like self-improving robots... do you think like any of those two scenarios might happen in your lifetime? Humans going on strike or like, self-improving robots?
Phil: so humans going on strike, certainly.
Michael: Against robots?
Phil: I don't know, if you imagine an amazon packing facility in which the workers aren't being overseen by a human manager, but by a computer, or by a a camera that has some AI ability to see how hard they're working, I can totally see the workers going on strike in that context, and are they going on strike against the robot? Well, sort of. The way we'd think of it is that they're going on strike against the owner of the robot. The owner of the camera, but unless the robots have like completely taken over, it's sort of the same thing, and even once even if robots do take over why would someone be less willing to go on strike because jeff bezos owns the camera than if the camera owns itself...
(If you enjoy those kind of technical videos with diagrams let me know in the comments so I make more of them.)