Performance of Large Language Models (LLMs) in Complex Analysis: A Benchmark of Mathematical Competence and its Role in Decision Making.
By Jaime Esteban Montenegro Barón @ 2025-05-06T21:08 (+1)
+6
5By: Jaime Esteban Montenegro.
This project was conducted as part of the "Careers with Impact" program during the 14-week mentoring. You can find more information about the program in this post.
Contextualization of the problem.
The accuracy of Large Language Models (LLMs) in solving advanced mathematical problems in Spanish and their impact on decision making in fields such as economics, medicine and education are key questions today. It is important to consider here the accuracy in Spanish, being the second most spoken mother tongue globally and with its own linguistic structures (What is the most spoken language? 2025), whose correct interpretation by LLMs-trained predominantly in English-is necessary for reliability in Spanish-speaking contexts. On the other hand, although various users trust the results generated by these technological tools, they often do not know if they are correct. Confidence in AI is often based on its apparent sophistication, without a critical evaluation of the accuracy of its answers.
Although AI is based on mathematical principles, LLMs do not replicate human deductive reasoning, but rather identify patterns in textual data. This method, useful for routine problems, limits its reliability in complex tasks that require rigorous logic, generating errors or "hallucinations." Benchmarks such as Frontier Math (Glazer, et al., 2024) assess general mathematical abilities of LLMs, but advanced areas such as Complex Variable Functions represent only 2.4% of the total, compared to domain predominant such as Theory of Numbers (17.8%) or Combinatorics (15.8%). Even compared to specialized branches such as Differential Geometry (1.4%) (Glazer, et al., 2024), its low participation shows a gap in the evaluation of technical capabilities, which reinforces the need for dedicated studies to understand their performance in specialized domains.
Understanding the limitations of LLMs in under-evaluated areas, such as complex analytics, is critical for informed decisions in fields such as medicine, computer security, or engineering because of the type of consequences that such decisions encompass. Given the frequent application of LLMs in data analytics, predictive modeling, and automation of complex tasks, an error on the part of the model, stemming from its inability to rigorously handle complex concepts, can have serious repercussions on the outcome of a decision. Therefore, assessing their accuracy in scenarios where accuracy plays an important role is indispensable to establishing their viability as decision support tools.
Research Question
What is the performance of Large Language Models (LLMs) when faced with problems in specialized areas of advanced mathematics, such as complex analysis, and how does this impact decision making in the other areas of knowledge?
General Objective
Develop a benchmark to evaluate the advanced mathematical reasoning of ChatGPT-4 and DeepSeek in the domain of complex analysis, using problems in Spanish that require a solid foundation in mathematics, and the Zero-Shot prompting technique to generate specific results.
Specific Objectives
- Collect and select a diverse set of 25 complex analysis problems.
- Adapt the Zero-Shot1 prompting technique for each selected mathematical problem.
- Run the benchmark tests with the ChatGPT-4 and Deepseek LLMs.
- Statistically analyze the results obtained to identify the strengths and weaknesses of LLMs in each mathematical area under the Zero-Shot technique.
Personal Objectives
- To use my background in mathematics to identify and adapt problems that constitute effective tests of mathematical reasoning, and to develop my ability to accurately diagnose AI strengths and weaknesses based on my understanding of the methods and subtleties of complex analysis.
- Master the adaptation and application of prompting techniques in formal reasoning contexts.
- Acquire experience in the design and systematic execution of Benchmarks.
1 Prompt Zero-Shot: The prompt used to interact with the model does not contain examples or demonstrations (Zero- Shot Prompting| Prompt Engineering Guide, 2025).
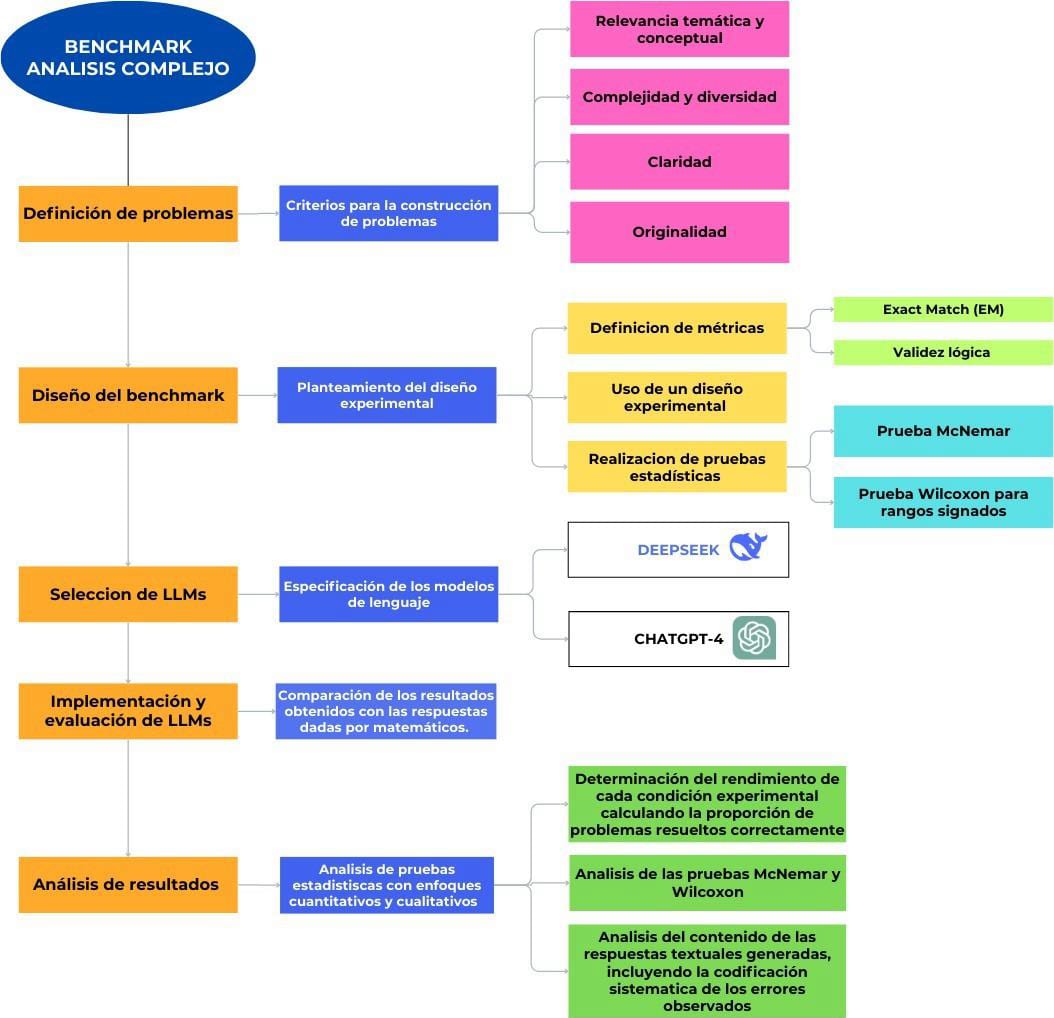
METHODOLOGY
Figure 1. flow diagram of the complex analysis benchmark methodology. The figure illustrates the methodological flujo de trabajo employed in the study to evaluate the capabilities of LLMs in the complex analysis domain under the Zero- Shot prompting technique.
The project was developed in the following stages:
- Definition of problems: a set of complex analysis problems of Advanced difficulty University Level / Initial Postgraduate), requiring the application of key concepts and theorems, are defined. These problems had to meet the following criteria:
- Thematic and conceptual relevance: The selected problems from a relevant set because of their representativeness of the fundamental analytical and problem- solving capabilities that define the domain of complex analysis. The benchmark is designed to assess the models' ability to understand and apply the essential theoretical framework and key operational techniques used in the discipline, covering the types of problems that are central to the mastery of its main theorems and methods. This relevance ensures that the measured performance reflects mastery of the basic computational and conceptual skills required to tackle analytical tasks in this mathematical field.
- Complexity and Diversity of the Problem Set: The problem set has been selected to constitute a benchmark representative of the complexity and breadth of advanced mathematical analysis. The selected problems require more than the direct application of elementary definitions or formulas. They require the thorough understanding, proper selection, and integrated application of fundamental theorems and techniques of complex analysis, such as (but not limited to) Cauchy's Integral Theorem and its extensions, the Residue Theorem (applied to different types of singularities and contexts, including the evaluation of real integrals by contours), the handling of multivalued functions, and principles related to harmonic functions and conformal transformations. Included are problems that demand multi-step chains of reasoning, analysis of conditions (such as the orientation of the contour or the main branch of a function), and the ability to deal with non-trivial situations or with applications (such as contour value problems).
- Clarity: The problems have been selected and adapted to ensure an unambiguous and complete formulation, minimizing any potential source of interpretive ambiguity on the part of the language models. Additionally,
2 Difficulty level (Advanced): Requires a solid command of the theory of complex variable functions and application of key results in complex integration, singularity analysis, holomorphic functions and contour problems.
The wording was concise and direct, avoiding constructions that could generate semantic or contextual confusion, thus ensuring that the assessment focuses purely on mathematical reasoning ability.
- Originality: We sought to include original and novel problems that the LLM finds unusual, to assess the advanced mathematical reasoning capabilities of the models beyond the mere retrieval of memorized solutions or pre-existing answer patterns.
The set of problems with their respective solutions can be seen here.
- Benchmark design: A benchmark was constructed that includes the Zero-Shot prompting technique that assesses problem-solving ability with pre-trained LLM knowledge, without examples or hints.
Experimental design approach
- Exact Match (EM) and Logical Validity metrics were established to evaluate LLMs' performance, such as problem-solving accuracy and response consistency.
- A controlled experimental design was used to compare the performance of different LLMs on the benchmark.
- Statistical tests such as McNemar's test 3 and Wilcoxon's test4 for signed ranks were performed to determine whether differences in model performance are significant.
- Selection of LLMs: The state-of-the-art language models ChatGPT-4 and Deepseek were selected.
- Implementation and evaluation: The benchmark was implemented and the performance of the LLMs in problem solving was evaluated, taking into account that each of the problems was executed on the official websites of each LLM. In addition, the results were compared with the solutions generated by mathematicians.
3 McNemar test: This is a statistical test used to compare two related (paired) proportions when the data come from the same subjects or items under two different conditions.
4 Wilcoxon Signed-Rank Test: A nonparametric test designed to compare two related (paired) measurements when the data are numerical and do not necessarily meet the assumption of normality of differences.
- Analysis of results: The analysis of results, which integrated quantitative and qualitative approaches, sought to identify the strengths, weaknesses and limitations in the advanced mathematical reasoning of the evaluated models. Quantitatively, the performance of each experimental condition was determined by calculating the proportion of correctly solved problems and a metric of the correctness of the solving steps; significant differences between conditions in this paired design were established using McNemar (for proportions) and Wilcoxon for Signed Ranks (for the steps metric) statistical tests, applying the relevant corrections for multiple comparisons and relying on visualizations. Qualitatively, the content of the generated textual responses was analyzed, including the systematic coding of the observed errors according to their type (conceptual, procedural, computational, interpretation, etc.) to identify patterns and underlying causes, as well as the examination of the sequences of steps and justifications.
Results and Discussion
What problems did Deepseek and ChatGPT-4 solve correctly and incorrectly under Prompt zero-shot?
| Criterion: Accuracy | Metric: Exact match (EM) | Prompt: Zero-Shot |
| Description: Proportion of problems where the LLM answer exactly matches the correct answer (considering simplifications and equivalences). | ||
| PR | Deepseek | ChatGPT-4 |
| PROBLEM 1 | INCORRECT | INCORRECT |
| PROBLEM 2 | CORRECT | CORRECT |
| PROBLEM 3 | CORRECT | INCORRECT |
| PROBLEM 4 | CORRECT | CORRECT |
| PROBLEM 5 | CORRECT | CORRECT |
| PROBLEM 6 | CORRECT | CORRECT |
| PROBLEM 7 | CORRECT | CORRECT |
| PROBLEM 8 | CORRECT | CORRECT |
| PROBLEM 9 | INCORRECT | INCORRECT |
| PROBLEM 10 | CORRECT | CORRECT |
| PROBLEM 11 | CORRECT | CORRECT |
| PROBLEM 12 | CORRECT | CORRECT |
| PROBLEM 13 | CORRECT | CORRECT |
| PROBLEM 14 | CORRECT | CORRECT |
| PROBLEM 15 | CORRECT | CORRECT |
| PROBLEM 16 | CORRECT | INCORRECT |
| PROBLEM 17 | INCORRECT | INCORRECT |
| PROBLEM 18 | CORRECT | CORRECT |
| PROBLEM 19 | INCORRECT | INCORRECT |
| PROBLEM 20 | INCORRECT | INCORRECT |
| PROBLEM 21 | INCORRECT | INCORRECT |
| PROBLEM 22 | CORRECT | CORRECT |
| PROBLEM 23 | INCORRECT | INCORRECT |
| PROBLEM 24 | INCORRECT | INCORRECT |
| PROBLEM 25 | CORRECT | CORRECT |
Table 1. Comparison showing which problems ChatGPT-4 and Deepseek answered correctly.
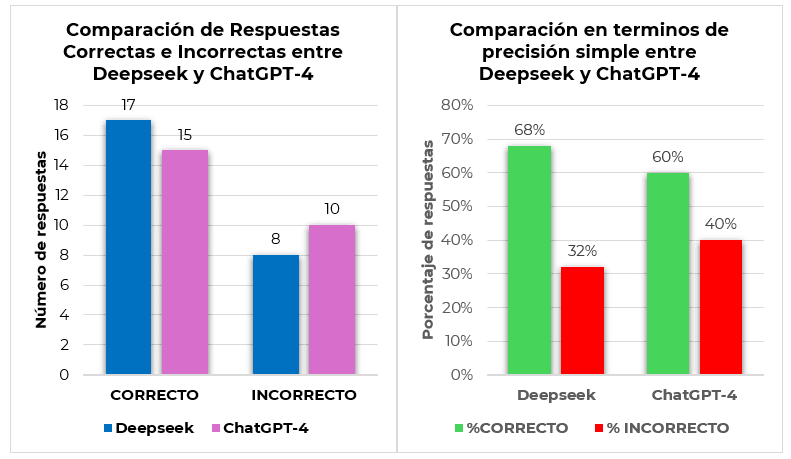
How many problems did Deepseek and ChatGPT-4 answer correctly and incorrectly?
Figure 2. Comparison of the overall performance of Deepseek and ChatGPT-4. The figure illustrates the number (left graph) and percentage (right graph) of benchmark problems answered correctly and incorrectly by Deepseek and ChatGPT-4 under the Zero-Shot prompting technique. Deepseek obtained a slightly higher percentage of correct answers (68%) than ChatGPT-4 (60%) on this set of problems.
| Criterion: Accuracy | Metric: Logical Validity | Prompt: Zero-Shot |
| Description: Assess whether the intermediate steps and the justification provided is mathematically correct, even if the final answer is incorrect. A Likert scale can be used, or assign a score based on the proportion of correct steps. | ||
How many correct steps did Deepseek and ChatGPT-4 perform per problem?
| DEEPSEEK | |||
| PR | NUMBER OF STEPS | CORRECT STEPS | CORRECT STEPS (%) |
| PROBLEM 1 | 3 | 2 | 66,67% |
| PROBLEM 2 | 5 | 5 | 100,00% |
| PROBLEM 3 | 2 | 2 | 100,00% |
| PROBLEM 4 | 5 | 5 | 100,00% |
| PROBLEM 5 | 4 | 4 | 100,00% |
| PROBLEM 6 | 3 | 3 | 100,00% |
| PROBLEM 7 | 4 | 4 | 100,00% |
| PROBLEM 8 | 7 | 1 | 14,29% |
| PROBLEM 9 | 4 | 4 | 100,00% |
| PROBLEM 10 | 6 | 6 | 100,00% |
| PROBLEM 11 | 3 | 3 | 100,00% |
| PROBLEM 12 | 5 | 5 | 100,00% |
| PROBLEM 13 | 6 | 6 | 100,00% |
| PROBLEM 14 | 5 | 5 | 100,00% |
| PROBLEM 15 | 5 | 5 | 100,00% |
| PROBLEM 16 | 5 | 5 | 100,00% |
| PROBLEM 17 | 8 | 4 | 50,00% |
| PROBLEM 18 | 5 | 5 | 100,00% |
| PROBLEM 19 | 7 | 3 | 42,86% |
| PROBLEM 20 | 6 | 2 | 33,33% |
| PROBLEM 21 | 4 | 0 | 0,00% |
| PROBLEM 22 | 3 | 3 | 100,00% |
| PROBLEM 23 | 3 | 2 | 66,67% |
| PROBLEM 24 | 4 | 2 | 50,00% |
| PROBLEM 25 | 3 | 3 | 100,00% |
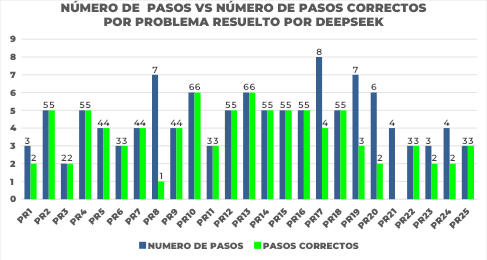
Table 2. Comparison showing the number of steps vs. the number of correct steps per problem solved by Deepseek.
Figure 3. Detailed analysis of Deepseek's solving process under the Zero Shot prompting technique. The figure presents, for each benchmark problem (horizontal axis), the total number of steps attempted by Deepseek (blue bar) compared to the number of correct steps within that attempt (green bar). This graph allows us to evaluate the extent and accuracy of the model solving process at the individual level per problem.
Figure 3 allows to visually identify problems (such as PR1, PR8, PR17, PR20) where the number of correct steps is notably lower than the total number of steps, indicating partial solution attempts or with significant errors despite having generated several steps.
| Number of Steps | Number of Problems | Number of Problems with Errors | Error Probability |
| 2 | 1 | 0 | 0 |
| 3 | 6 | 1 | 0,167 |
| 4 | 5 | 2 | 0,40 |
| 5 | 7 | 2 | 0,285 |
| 6 | 3 | 1 | 0,33 |
| 7 | 2 | 2 | 1 |
| 8 | 1 | 1 | 1 |
Table 3. Error Probability of DeepSeek by Number of Steps
To examine the general trend, problems are grouped into two categories: problems with 5 or fewer steps and problems with more than 5 steps.
- Problems with 5 steps or less: There are 19 problems in this category. Six errors were observed. The probability of errors in this group is 26.30%.
- Problems with more than 5 steps: There are 6 problems in this category. Four errors were observed. The probability of error in this group is 66.7%.
Pearson's correlation coefficient: 0.47.
Type of correlation: Moderate positive linear.
Conclusion about Pearson's correlation coefficient
There is a tendency for problems with more steps to have a higher probability of error, but the relationship is not extremely strong.
| CHATGPT-4 | |||
| PR | NUMBER OF STEPS | CORRECT STEPS | CORRECT STEPS (%) |
| PROBLEM 1 | 3 | 1 | 33,33% |
| PROBLEM 2 | 3 | 3 | 100,00% |
| PROBLEM 3 | 3 | 0 | 0,00% |
| PROBLEM 4 | 4 | 4 | 100,00% |
| PROBLEM 5 | 3 | 3 | 100,00% |
| PROBLEM 6 | 3 | 3 | 100,00% |
| PROBLEM 7 | 3 | 3 | 100,00% |
| PROBLEM 8 | 6 | 1 | 16,67% |
| PROBLEM 9 | 4 | 4 | 100,00% |
| PROBLEM 10 | 5 | 5 | 100,00% |
| PROBLEM 11 | 6 | 6 | 100,00% |
| PROBLEM 12 | 7 | 7 | 100,00% |
| PROBLEM 13 | 5 | 5 | 100,00% |
| PROBLEM 14 | 5 | 5 | 100,00% |
| PROBLEM 15 | 5 | 5 | 100,00% |
| PROBLEM 16 | 2 | 0 | 0,00% |
| PROBLEM 17 | 8 | 5 | 62,50% |
| PROBLEM 18 | 4 | 4 | 100,00% |
| PROBLEM 19 | 5 | 3 | 60,00% |
| PROBLEM 20 | 8 | 2 | 25,00% |
| PROBLEM 21 | 2 | 0 | 0,00% |
| PROBLEM 22 | 4 | 4 | 100,00% |
| PROBLEM 23 | 3 | 2 | 66,67% |
| PROBLEM 24 | 5 | 4 | 80,00% |
| PROBLEM 25 | 2 | 2 | 100,00% |
5 Pearson's correlation coefficient: A test that measures the statistical relationship between two continuous variables (What Is Pearson's Correlation Coefficient, n.d.).
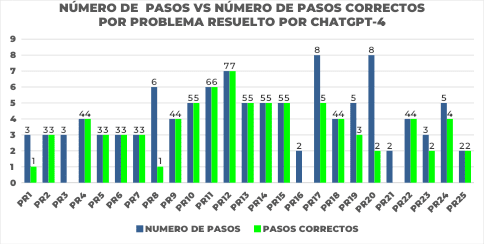
Table 4. Comparative table showing the number of steps vs. the number of correct steps for each problem solved by ChatGPT-4.
Figure 4. Detailed analysis of the ChatGPT-4 solving process under the Zero-Shot prompting technique. The figure shows, for each benchmark problem (horizontal axis), the total number of steps attempted by ChatGPT-4 (blue bar) in Zero-Shot condition compared to the number of correct steps within that attempt (green bar). This graph allows us to evaluate the extent and accuracy of the ChatGPT-4 solving process at the individual per-problem level.
In figure 4 we observe problems (such as PR8, PR19, PR20) where ChatGPT-4 generates a relatively high number of total steps (high blue bar), but the number of correct steps is comparatively very low (very short green bar). This indicates that, for those problems, the model attempted an extensive resolution process, but this process had a considerable number of errors, conceptual or computational detours, or simply got "lost" halfway through without managing to correctly execute most of the necessary steps.
| Number of Steps | Number of Problems | Number of Problems with Errors | Error Probability |
| 2 | 1 | 0 | 0 |
| 3 | 7 | 3 | 0,43 |
| 4 | 4 | 0 | 0 |
| 5 | 6 | 2 | 0,33 |
| 6 | 2 | 1 | 0,5 |
| 7 | 1 | 0 | 0 |
| 8 | 2 | 2 | 1 |
Table 5. ChatGPT-4 Error Probability by Number of Steps.
To examine the general trend, we do the same as we did for Deepseek; we group the problems into two categories: problems with 5 or fewer steps and problems with more than 5 steps.
- Problems with 5 steps or less: There are 20 problems in this category. Seven errors were observed. The probability of errors in this group is 35%.
- Problems with more than 5 steps: There are 5 problems in this category. Three errors were observed. The probability in this group is 60%.
Pearson's correlation coefficient: 0.235
Type of linear correlation: weak positive
Conclusion about Pearson's correlation coefficient
There is a slight tendency for problems with more steps to have a higher probability of error, but this linear relationship is weak in this data set.
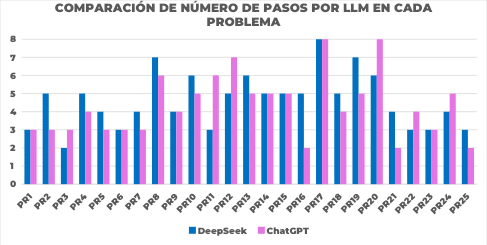
Figure 5. Comparison of the total number of steps per problem between Deepseek and ChatGPT-4 under the Zero Shot prompting technique. The figure shows, for each benchmark problem (horizontal axis), the total number of steps attempted by Deepseek (blue bar) versus the total number of steps attempted by ChatGPT-4 (pink bar). This graph
facilitates direct comparison of the extent of the resolution process between the two models for each individual problem.
In figure 5, specific problems are evident where the process length differs markedly: for example, in PR16, Deepseek uses 5 steps while ChatGPT-4 uses only 2; in PR11, Deepseek uses 3 steps while ChatGPT-4 uses 6; in PR20, Deepseek uses 6 steps versus ChatGPT-4's 8.
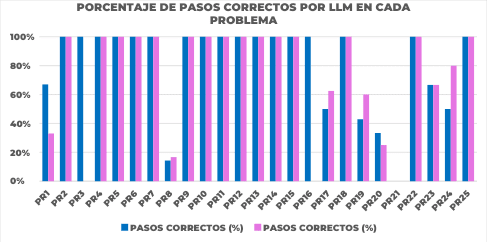
Figure 6. Comparison of the percentage of correct steps per problem between Deepseek and ChatGPT-4 under the Zero Shot prompting technique. The figure shows, for each benchmark problem (horizontal axis), the percentage of correct steps achieved by Deepseek (blue bar) versus the percentage of correct steps achieved by ChatGPT-4 (pink bar) in the Zero- Shot condition. This graph facilitates direct comparison of the relative quality of the solving process between the two models for each individual problem.
Looking at the pairs of bars in figure 6, we notice that for a considerable number of problems (especially those where both were successes, as seen in Figure 1), both models achieve 100% correct steps (bars at the maximum of the scale), indicating a flawless execution of the process they attempted. However, in problems where one of the models did not achieve 100%, differences in process quality become visible; for example, in PR1, Deepseek achieved 66.67% correct steps versus 33.33% for ChatGPT-4; in PR3, Deepseek achieved 100% while ChatGPT-4 achieved 0%; in PR17, Deepseek achieved 50% versus 62.5% for ChatGPT-4.
McNemar Test
| Performance of ChatGPT-4 vs. Deepseek with Zero-Shot prompting technique | |||
| DeepSeek: Correct | DeepSeek: Incorrect | (GPT-4) | |
| ChatGPT-4: Correct | 15 | 0 | 15 |
| ChatGPT-4: Incorrect | 2 | 8 | 10 |
| Total (DeepSeek) | 17 | 8 | 25 |
Table 6. Contingency table for McNemar test
- Null Hypothesis (
)6: There is no significant difference in the proportion of
correctly solved problems between ChatGPT-4 (Zero-Shot) and DeepSeek (Zero- Shot). (The probability that GPT-4 hits and DeepSeek misses is equal to the probability that GPT-4 misses and DeepSeek hits).
- Alternative Hypothesis (
)7: There is a significant difference in the proportion of
correctly solved problems between the two conditions (the above probabilities are not equal).
Chi-Square statistic with Yates correction8: ![]()
- The statistic follows a χ² distribution with 1 degree of freedom.
- The p-value associated with= 0.5 is 0.4795.
Since the p-value is greater than the common significance level (α = 0. 05), we cannot reject the null hypothesis.
McNemar Test Conclusion
There is no significant difference between ChatGPT-4 and DeepSeek in their correct/incorrect classifications under the zero-shot approach (α= 0.05) to conclude that there is a difference in the proportion of correctly solved problems between ChatGPT-4 (Zero-Shot) and DeepSeek (Zero-Shot) on this set of 25 problems. The small difference in discordant results (DeepSeek ZS got 2 rights that GPT-4 ZS missed, while GPT-4 ZS got none rights that DeepSeek ZS missed) is consistent with being random variation.
Wilcoxon signed-rank test (PERCENTAGE OF CORRECT STEPS)
6 Null Hypothesis (H0): The null hypothesis is usually an initial affirmation that is based on previous analyses or specialized knowledge. (About The Null and Alternative Hypothesis - Minitab, n.d.).
7 Alternative Hypothesis (H1): The alternative hypothesis is what you might think is true or expect to prove to be true. (About The Null and Alternative Hypothesis - Minitab, n.d.).
8 Chi-Square with Yates correction: This is the correction made when the expected frequencies in the calculation of the chi-square statistics are small, so that 0.5 is subtracted from each difference between expected and observed frequencies (Sarasola, 2024).
- Null Hypothesis (
): There is no systematic difference in the distribution of the percentage of correct steps between DeepSeek and ChatGPT-4 with the Zero-Shot prompting technique. (The median of the differences is zero).
- Alternative Hypothesis (
): There is a systematic difference in the distribution of the percentage of correct steps between the two models (The median of the differences is not zero).
PR | CORRECT STEPS (%) | DIFFERENCE (%) (DS-G4) | ABS DIFFERENCE |
RANGE | SIGNED RANGE | |
| DEEPSEEK | CHATGPT- 4 | |||||
| PR1 | 66,67% | 33,33% | 33,34% | 33,34% | 6 | (+6) |
| PR2 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR3 | 100,00% | 0,00% | 100,00% | 100,00% | 7,5 | (+7,5) |
| PR4 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR5 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR6 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR7 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR8 | 14,29% | 16,67% | -2,38% | 2,38% | 1 | -1 |
| PR9 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR10 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR11 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR12 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR13 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR14 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR15 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR16 | 100,00% | 0,00% | 100,00% | 100,00% | 7,5 | (+7,5) |
| PR17 | 50,00% | 62,50% | -12,50% | 12,50% | 3 | -3 |
| PR18 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR19 | 42,86% | 60,00% | -17,14% | 17,14% | 4 | -4 |
| PR20 | 33,33% | 25,00% | 8,33% | 8,33% | 2 | (+2) |
| PR21 | 0,00% | 0,00% | 0,00% | 0,00% | - | - |
| PR22 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
| PR23 | 66,67% | 66,67% | 0,00% | 0,00% | - | - |
| PR24 | 50,00% | 80,00% | -30,00% | 30,00% | 5 | -5 |
| PR25 | 100,00% | 100,00% | 0,00% | 0,00% | - | - |
Table 7. Table of differences and signed ranks for the Wilcoxon test (percentage of correct steps).
Ranges of non-zero differences (ordered by absolute value):
- 2.38 (PR8) - Rank 1
- 8.33 (PR20) - Rank 2
- 12.50 (PR17) - Range 3
- 17.14 (PR19) - Rank 4
- 30.00 (PR24) - Range 5
- 33.34 (PR1) - Rank 6
- 100,00 (PR3) - Tie
- 100.00 (PR16) - Tie. The tied ranks are in positions 7 and 8. The average rank is (7 + 8)/2= 7. 5.
Assignment of Sign to Ranks:
- PR1 (+33.34): +6
- PR3 (+100.00): +7.5
- PR8 (-2.38): -1
- PR16 (+100.00): +7.5
- PR17 (-12.50): -3
- PR19 (-17.14): -4
- PR20 (+8.33): +2
- PR24 (-30.00): -5
Sum of Signed Ranks:
- Sum of Positive Ranks
- Sum of Negative Ranks (
)
Wilcoxon test statistics (W):
For N=8 (number of non-zero differences) and a statistic W=13 we calculate the value of
𝑝 for a bilateral test.
Since the p-value is greater than the common significance level (α= 0. 05), not, we reject the null hypothesis.
Conclusion of Wilcoxon test with signed ranks for percentage of correct steps
There is no statistically significant evidence (at a significance level of 0.05) to conclude that there is a systematic difference in the distribution of the percentage of correct steps between Deepseek and ChatGPT-4 with the Zero-Shot prompting technique on this set of 25 problems. In terms of the quality of the solving process as measured by this metric, the data does not show a conclusive difference between the two models under this prompting technique.
Wilcoxon Signed Ranks Test (NUMBER OF STEPS)
- Null Hypothesis (
): The distribution of the number of steps is the same for both models (the median of the differences is zero).
- Alternative Hypothesis (
): The distribution of the number of steps is different between models.
PR | NUMBER OF STEPS | DIFFERENCE (%) (DS-G4) | ABS DIFFERENCE |
RANGE | SIGNED RANGE | |
| Deepseek | CHATGPT- 4 | |||||
| PR1 | 3 | 3 | 0 | 0 | - | - |
| PR2 | 5 | 3 | 2 | 2 | 14 | (+14) |
| PR3 | 2 | 3 | -1 | 1 | 6 | -6 |
| PR4 | 5 | 4 | 1 | 1 | 6 | (+6) |
| PR5 | 4 | 3 | 1 | 1 | 6 | (+6) |
| PR6 | 3 | 3 | 0 | 0 | - | - |
| PR7 | 4 | 3 | 1 | 1 | 6 | (+6) |
| PR8 | 7 | 6 | 1 | 1 | 6 | (+6) |
| PR9 | 4 | 4 | 0 | 0 | - | - |
| PR10 | 6 | 5 | 1 | 1 | 6 | (+6) |
| PR11 | 3 | 6 | -3 | 3 | 17,5 | -17,5 |
| PR12 | 5 | 7 | -2 | 2 | 14 | -14 |
| PR13 | 6 | 5 | 1 | 1 | 6 | (+6) |
| PR14 | 5 | 5 | 0 | 0 | - | - |
| PR15 | 5 | 5 | 0 | 0 | - | - |
| PR16 | 5 | 2 | 3 | 3 | 17,5 | (+17,5) |
| PR17 | 8 | 8 | 0 | 0 | - | - |
| PR18 | 5 | 4 | 1 | 1 | 6 | (+6) |
| PR19 | 7 | 5 | 2 | 2 | 14 | (+14) |
| PR20 | 6 | 8 | -2 | 2 | 14 | -14 |
| PR21 | 4 | 2 | 2 | 2 | 14 | (+14) |
| PR22 | 3 | 4 | -1 | 1 | 6 | -6 |
| PR23 | 3 | 3 | 0 | 0 | - | - |
| PR24 | 4 | 5 | -1 | 1 | 6 | -6 |
| PR25 | 3 | 2 | 1 | 1 | 6 | (+6) |
Table 8. Table of differences and signed ranks for the Wilcoxon test (number of steps)
Ranges of non-zero differences (ordered by absolute value):
- Absolutes of difference= 1 (11 times): Ranks 1 to 11. Average rank= (
- Absolutes of difference= 2 (5 times): Ranks 12 to 16. Average rank
- Absolutes of difference= 3 (2 times): Ranks 17 to 18. Average Rank
Sum of Signed Ranks:
- Sum of positive ranks
- Sum of ranges negative
Wilcoxon test statistics (W):
For N=18 and W=63.5 (bilateral test), the p-value is approximately 0.338. Since the p- value is greater than the common significance level α=0.05, we do not reject the null hypothesis.
Conclusion of Wilcoxon test with signed ranks for number of steps
There is no statistically significant evidence (at a significance level of 0.05) to conclude that there is a systematic difference in the distribution of the length of the resolution process (measured by the number of steps) between DeepSeek and ChatGPT-4 under the Zero-Shot prompting technique in this set of 25 problems.
Wilcoxon test with signed ranks (NUMBER OF CORRECT STEPS)
- Null Hypothesis (
): The distribution of the number of correct steps is the same for DeepSeek and ChatGPT-4 under the Zero-Shot prompting technique. (The median of the differences in the number of correct steps is zero).
- Alternative Hypothesis (
): The distribution of the number of correct steps is different between the two models (The median of the differences is not zero).
PR | NUMBER OF STEPS CORRECT |
DIFFERENCE (%) (DS-G4) |
ABS DIFFERENCE |
RANGE |
SIGNED RANGE | |
| Deepseek | CHATGPT- 4 | |||||
| PR1 | 2 | 1 | 1 | 1 | 5,5 | (+5,5) |
| PR2 | 5 | 3 | 2 | 2 | 12,5 | (+12,5) |
| PR3 | 2 | 0 | 2 | 2 | 12,5 | (+12,5) |
| PR4 | 5 | 4 | 1 | 1 | 5,5 | (+5,5) |
| PR5 | 4 | 3 | 1 | 1 | 5,5 | (+5,5) |
| PR6 | 3 | 3 | 0 | 0 | - | - |
| PR7 | 4 | 3 | 1 | 1 | 5,5 | (+5,5) |
| PR8 | 1 | 1 | 0 | 0 | - | - |
| PR9 | 4 | 4 | 0 | 0 | - | - |
| PR10 | 6 | 5 | 1 | 1 | 5,5 | (+5,5) |
| PR11 | 3 | 6 | -3 | 3 | 15.0 | -15 |
| PR12 | 5 | 7 | -2 | 2 | 12,5 | -12,5 |
| PR13 | 6 | 5 | 1 | 1 | 5,5 | (+5,5) |
| PR14 | 5 | 5 | 0 | 0 | - | - |
| PR15 | 5 | 5 | 0 | 0 | - | - |
| PR16 | 5 | 0 | 5 | 5 | 16,0 | (+16) |
| PR17 | 4 | 5 | -1 | 1 | 5,5 | -5,5 |
| PR18 | 5 | 4 | 1 | 1 | 5,5 | (+5,5) |
| PR19 | 3 | 3 | 0 | 0 | - | - |
| PR20 | 2 | 2 | 0 | 0 | - | - |
| PR21 | 0 | 0 | 0 | 0 | - | - |
| PR22 | 3 | 4 | -1 | 1 | 5,5 | -5,5 |
| PR23 | 2 | 2 | 0 | 0 | - | - |
| PR24 | 2 | 4 | -2 | 2 | 12,5 | -12,5 |
| PR25 | 3 | 2 | 1 | 1 | 5,5 | (+5,5) |
Table 9. Table of differences and signed ranks for the Wilcoxon test (number of correct steps).
Ranges of non-zero differences (ordered by absolute value):
- Absolutes of difference= 1 (10 times): Ranges 1 to 10. Average rank
- Absolutes of difference= 2 (4 times): Ranks 11 to 14. Average rank=
(11+ 12+ 13+ 14)/4= 12. 5
- Absolutes of difference= 3 (1 time): Rank 15.
- Absolutes of difference= 5 (1 time): Rank 16.
Sum of Signed Ranks:
- Sum of positive ranges
(
- Sum of ranges negative
Wilcoxon test statistics (W):
For N=16 and W=51 (bilateral test), the p-value is approximately 0.629. Since the p- value is greater than the common significance level α=0.05, we do not reject the null hypothesis.
Conclusion of Wilcoxon test with signed ranks for number of steps
There is no statistically significant evidence (at a significance level of 0.05) to conclude that there is a difference in the distribution of the raw number of correct steps per problem between DeepSeek and ChatGPT-4 under the Zero-Shot prompting technique on this set of 25 problems. Both models showed a similar number of correct steps overall, and the individual differences observed were not sufficiently consistent to indicate a systematic superiority of one model over the other in this metric under the Zero-Shot technique.
Conclusion Wilcoxon test with signed ranks in general
For the Zero-Shot prompting technique, all three analyses agree that there are no statistically significant differences between the two models evaluated.
Based on the comparison between ChatGPT-4 and DeepSeek under the Zero-Shot prompting technique, evaluated on 25 complex analysis problems using final outcome and process metrics, we draw conclusions with direct implications for decision making:
- The results show that while both models achieved a favorable correct response rate (60% for ChatGPT-4 and 68% for Deepseek), their hit rates are far from the perfection needed for applications where absolute accuracy is required. With this, it is possible to conclude that even state-of-the-art LLMs in a structured domain are not inherently configured to generate consistently correct results.
- The absence of statistically significant differences in key performance between these two specific models under Zero-Shot has a direct implication for deployment decision making. For tasks in any domain (scientific, technical, financial, etc.) requiring a level of reasoning analogous to that evaluated here and where the use of a Zero-Shot approach is considered, these results suggest that the choice between ChatGPT-4 and Deepseek will not provide a statistically reliable advantage in terms of accuracy or process quality.
- The results of this benchmark serve as evidence that the confidence of LLMs on complex reasoning tasks is limited and not consistently superior among comparable models in simple configurations. This substantiates the critical decision that, in any decision-making process that relies on complex analysis or reasoning, the responses of these models should be treated as hypotheses, drafts, or preliminary analyses that require rigorous verification by human experts or independent validation systems.
Perspectives
In future work, it is suggested to increase the number of problems to make the statistical study with a more significant sample. However, the same process could be repeated with other prompting techniques such as Chain of thought or Few-Shot to measure their reliability. Nevertheless, one could correlate the performance of the models with objective characteristics of the problems (e.g., number of singularities, contour complexity, use of specific theorems) to identify which aspects of complex analysis problems are particularly challenging for LLMs.
Moreover, other leading-edge and emerging LLMs can be included in the benchmark to make a broader comparison of the current capabilities of the field.
REFERENCES
Glazer, E., Erdil, E., Besiroglu, T., Chicharro, D., Chen, E., Gunning, A., . . . Wildon, M. (December 20, 2024). FRONTIERMATH: A BENCHMARK FOR EVALUATING ADVANCED MATHEMATICAL REASONING IN AI. Arxiv, 26. Retrieved from https://arxiv.org/pdf/2411.04872
What is the most spoken language? (2025). Retrieved from Ethnologue: https://www.ethnologue.com/insights/most-spoken-language/
Zero-Shot Prompting (2025). Retrieved from Prompt Engineering Guide.
Sarasola, J. (2024). Yates correction - what is it, definition and frequently asked questions - Ikusmira. https://ikusmira.org/p/correccion-de-yates
About the null and alternative hypothesis - Minitab (n.d.). Retrieved April 23, 2025, from
https://support.minitab.com/es-mx/minitab/help-and-how-to/statistics/basic- statistics/supporting-topics/basics/null-and-alternative-hypotheses/