A new way to estimate welfare growth

By trammell @ 2025-09-12T16:37 (+17)

I've just started a Substack, and this is a linkpost for the first entry. It's about a way to estimate welfare growth—I’ll say “utility growth”—using nominal interest rates and the value of statistical life (VSL).^[1]

The idea is, interest rates let us compare how much utility you can buy with a dollar at different points in time, and the VSL at time t is how many dollars people at t are willing to pay for a small reduction in mortality risk at t. Putting these together, we should be able to say how quickly utility has grown over time, on a ratio scale where 0 is the utility of death.

When we do this, we conclude that utility has grown much more quickly than commonly supposed. In fact we conclude that it has grown implausibly quickly, but maybe there is something to learn the exercise nonetheless.

Summary

The most common way to measure utility growth, at least for economists, is to

try to sort out the shape of a typical utility function in consumption, u(c) (and maybe some other variables, like health and leisure), and
to put a number to how quickly consumption (and maybe the other variables) has grown.

But we can't possibly measure all the things that affect people's wellbeing, and even the things we act like we can measure (like "consumption") I think we really can't, since what a unit of consumption is varies from period to period as the set of available products changes.

So here's a simple thing we can do instead.

Let be the function from nominal consumption per year (c) to flow utility (u)in year t, where u = 0 denotes the utility assigned to death during year t, for some person. Note that the time-dependency of the utility function can account for inflation, or any other changes in the relationship between utility and nominal consumption.
Let $u_{t}^{'} \equiv \frac{d}{d c_{t}} u (c_{t}, t) .$
Let $E U_{t}$ denote the total expected utility a person at t expects to enjoy from t onward (if she doesn't die at t).

Then the value of statistical life for this person at t (VSL_t), given that she enjoys nominal consumption c_t at t, is given by

{VSL}_{t} = \frac{E U_{t}}{u_{t}^{'}} .

For this person to be indifferent between saving a little more and saving a little less at t, we must have g_u',t = 𝛿-r_t, where g_u',t is the proportional growth rate of her marginal utility in nominal consumption at t, 𝛿 is her discount rate, and r_t is the nominal interest rate at t. So, rearranging the above and taking growth rates,

g_{E U, t} = g_{VSL, t} + δ - r_{t} .

To emphasize, this relationship follows mechanically from the fact that, at each point in time, the VSL is the willingness to pay to reduce mortality risk. I am assuming that people maximize expected lifetime utility, but I making no assumptions at all about u(c,t) except that, at each t, it is locally differentiable in c around c_t. Everything here is compatible with any model of changing products, tastes, leisure, health, habits, "keeping up with the Joneses", price indices, utility derived from relationships, and so on.

If we estimate $g_{E U, t}$ on the basis of observed VSLs and interest rates over time, we get very, very high numbers, even if we assume that investors have been using a discount rate of 0%. Here is what I get for the US from 1940 to 1980. The last column is what you get if you take the more conventional approach, assuming (i) that utility is logarithmic in "real consumption" (as defined by the BEA) and (ii) that you need $1000. As explained in the full post, within reason, I've chosen the assumptions and data sources to make utility grow as quickly as possible on the "conventional approach" and as slowly as possible on the "VSL approach", but the gap is still enormous.

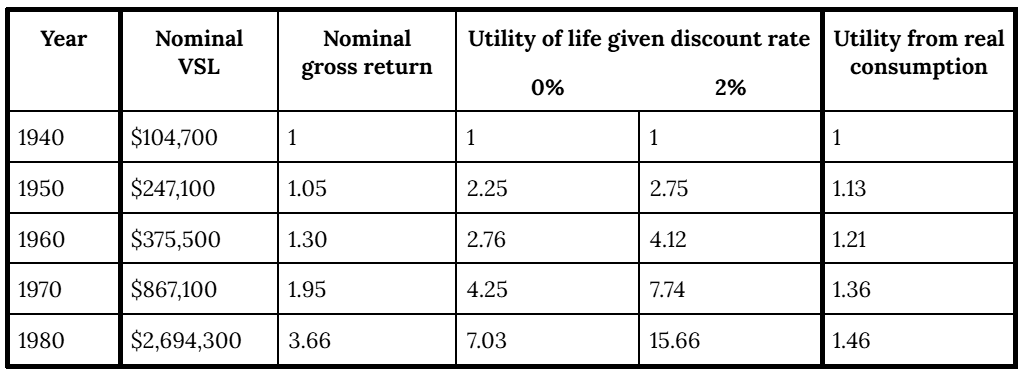
I'm not sure what's going on here. As explained in the post, I think the idea that we were 7 (let alone 15.66) times better off in 1980 than in 1940 is completely implausible—it implies that someone in 1980 would rather take an 85% chance of death than go back in time to 1940—but most of the ideas that come to mind for minimizing the discrepancy don't put much of a dent in it, or even make it worse. I expect a big part of the story is just that we've gotten more squeamish about death over time for reasons independent of improved life (which would be an interesting finding in its own right).

Nevertheless, presumably to some extent this is also evidence that people have been getting better off over time more quickly than is commonly supposed. And if so, this has all sorts of implications. E.g., insofar as we attribute all this utility growth to economic growth, then economic growth is more valuable than we would otherwise have thought, at least for humans in the medium term.

^{^}
According to GPT-5, the approach seems to be novel, despite its simplicity.